在引人入胜的大型语言模型(LLM)世界中,模型架构、数据处理和优化备受关注。然而,在文本生成中发挥关键作用的解码策略,如beam search,却常被忽视。在本文中,我们将通过深入研究greedy search 、 beam search, 和 sampling techniques with top-k and nucleus sampling,探索 LLM 如何生成文本。
Background
首先,让我们从一个例子开始。我们将文本“I have a dream”输入 GPT-2 模型,并要求它生成接下来的五个 token(单词或子词)。
from transformers import GPT2LMHeadModel, GPT2Tokenizer
import torch
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model = GPT2LMHeadModel.from_pretrained('gpt2').to(device)
tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
model.eval()
text = "I have a dream"
input_ids = tokenizer.encode(text, return_tensors='pt').to(device)
outputs = model.generate(input_ids, max_length=len(input_ids.squeeze())+5)
generated_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print(f"Generated text: {generated_text}")
Generated text: I have a dream of being a doctor.
人们普遍存在一个误解,认为像 GPT-2 这样的 LLMs 直接生成所有文本。事实并非如此,LLMs 计算 logits,即分配给其词汇表中每个可能 token 的分数。以下是该过程的说明性分解:

分词器(在此例中为 Byte-Pair Encoding)将输入文本中的每个 token 转换为相应的 token ID。然后,GPT-2 使用这些 token ID 作为输入,并尝试预测下一个最可能的 token。最后,模型生成 logits,这些 logits 通过 softmax 函数转换为概率。
| 例如,模型将“of”作为“I have a dream”之后的下一个 token 的概率分配为 17%。这个输出本质上代表了序列中潜在下一个 token 的排名列表。更正式地说,我们将其概率表示为 $P(\text{of } | \text{ I have a dream}) = 17\% $。 |
自回归模型如 GPT 根据前一个词序列预测下一个词。考虑一个词序列 $w = (w_1, w_2, \ldots, w_t)$ ,这个序列的联合概率 P(w) 可以分解为: \(\begin{align} P(w) &= P(w_1, w_2, \ldots, w_t) \\ &= P(w_1) P(w_2 | w_1) P(w_3 | w_2, w_1) \ldots P(w_t | w_1, \ldots, w_{t-1}) \\ &= \prod_{i=1}^t P(w_i | w_1, \dots, w_{i-1}). \end{align}\) 对于序列中的每个词 $w_i , P(w_i | w_1, \ldots, w_{i-1})$ 表示在所有前序词$ (w_1, \ldots, w_{i-1})$ 的条件下 w_i 的条件概率。GPT-2 为其词汇表中的 50,257 个词计算这个条件概率。
这就引出了问题:我们如何利用这些概率来生成文本?这就是解码策略,如贪婪搜索和束搜索发挥作用的地方。
Greedy Search
贪婪搜索是一种解码方法,它在每一步都选择最可能的标记作为序列中的下一个标记。简单来说,它只在每个阶段保留最可能的标记,丢弃所有其他潜在选项。以我们的例子为例:
- Step 1: Input: “I have a dream” → Most likely token: ” of”
- Step 2: Input: “I have a dream of” → Most likely token: ” being”
- Step 3: Input: “I have a dream of being” → Most likely token: ” a”
- Step 4: Input: “I have a dream of being a” → Most likely token: ” doctor”
- Step 5: Input: “I have a dream of being a doctor” → Most likely token: “.”
虽然这种方法听起来很直观,但需要注意的是贪婪搜索是短视的:它在每一步只考虑最可能的标记,而不考虑对整个序列的总体影响。这种特性使其快速高效,因为它不需要跟踪多个序列,但也意味着它可能会错过那些可能由稍低概率的下一个标记产生的更好序列。
接下来,我们使用 graphviz 和 networkx 来说明贪婪搜索的实现。我们选择得分最高的 ID,计算其日志概率(我们取对数以简化计算),并将其添加到树中。我们将重复此过程五次。
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import time
def get_log_prob(logits, token_id):
# Compute the softmax of the logits
probabilities = torch.nn.functional.softmax(logits, dim=-1)
log_probabilities = torch.log(probabilities)
# Get the log probability of the token
token_log_probability = log_probabilities[token_id].item()
return token_log_probability
def greedy_search(input_ids, node, length=5):
if length == 0:
return input_ids
outputs = model(input_ids)
predictions = outputs.logits
# Get the predicted next sub-word (here we use top-k search)
logits = predictions[0, -1, :]
token_id = torch.argmax(logits).unsqueeze(0)
# Compute the score of the predicted token
token_score = get_log_prob(logits, token_id)
# Add the predicted token to the list of input ids
new_input_ids = torch.cat([input_ids, token_id.unsqueeze(0)], dim=-1)
# Add node and edge to graph
next_token = tokenizer.decode(token_id, skip_special_tokens=True)
current_node = list(graph.successors(node))[0]
graph.nodes[current_node]['tokenscore'] = np.exp(token_score) * 100
graph.nodes[current_node]['token'] = next_token + f"_{length}"
# Recursive call
input_ids = greedy_search(new_input_ids, current_node, length-1)
return input_ids
# Parameters
length = 5
beams = 1
# Create a balanced tree with height 'length'
graph = nx.balanced_tree(1, length, create_using=nx.DiGraph())
# Add 'tokenscore', 'cumscore', and 'token' attributes to each node
for node in graph.nodes:
graph.nodes[node]['tokenscore'] = 100
graph.nodes[node]['token'] = text
# Start generating text
output_ids = greedy_search(input_ids, 0, length=length)
output = tokenizer.decode(output_ids.squeeze().tolist(), skip_special_tokens=True)
print(f"Generated text: {output}")
Generated text: I have a dream of being a doctor.
我们的贪婪搜索生成的文本与 transformers 库生成的文本相同:“I have a dream of being a doctor.” 让我们可视化我们创建的树。
import matplotlib.pyplot as plt
import networkx as nx
import matplotlib.colors as mcolors
from matplotlib.colors import LinearSegmentedColormap
def plot_graph(graph, length, beams, score):
fig, ax = plt.subplots(figsize=(3+1.2*beams**length, max(5, 2+length)), dpi=300, facecolor='white')
# Create positions for each node
pos = nx.nx_agraph.graphviz_layout(graph, prog="dot")
# Normalize the colors along the range of token scores
if score == 'token':
scores = [data['tokenscore'] for _, data in graph.nodes(data=True) if data['token'] is not None]
elif score == 'sequence':
scores = [data['sequencescore'] for _, data in graph.nodes(data=True) if data['token'] is not None]
vmin = min(scores)
vmax = max(scores)
norm = mcolors.Normalize(vmin=vmin, vmax=vmax)
cmap = LinearSegmentedColormap.from_list('rg', ["r", "y", "g"], N=256)
# Draw the nodes
nx.draw_networkx_nodes(graph, pos, node_size=2000, node_shape='o', alpha=1, linewidths=4,
node_color=scores, cmap=cmap)
# Draw the edges
nx.draw_networkx_edges(graph, pos)
# Draw the labels
if score == 'token':
labels = {node: data['token'].split('_')[0] + f"\n{data['tokenscore']:.2f}%" for node, data in graph.nodes(data=True) if data['token'] is not None}
elif score == 'sequence':
labels = {node: data['token'].split('_')[0] + f"\n{data['sequencescore']:.2f}" for node, data in graph.nodes(data=True) if data['token'] is not None}
nx.draw_networkx_labels(graph, pos, labels=labels, font_size=10)
plt.box(False)
# Add a colorbar
sm = plt.cm.ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])
if score == 'token':
fig.colorbar(sm, ax=ax, orientation='vertical', pad=0, label='Token probability (%)')
elif score == 'sequence':
fig.colorbar(sm, ax=ax, orientation='vertical', pad=0, label='Sequence score')
plt.show()
# Plot graph
plot_graph(graph, length, 1.5, 'token')
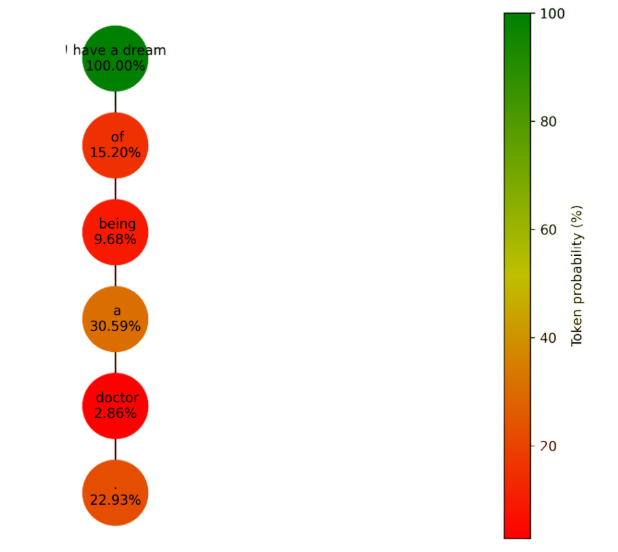
在这个图中,顶节点存储输入的 token(因此概率为 100%),而其他所有节点代表生成的 token。尽管这个序列中的每个 token 在预测时都是最可能的,但”being”和”doctor”分别被分配了相对较低的 9.68%和 2.86%的概率。这表明我们最初预测的 token “of”可能不是最合适的选择,因为它导致了不太可能的”being”。
Beam Search
与仅考虑下一个最可能标记的贪婪搜索不同,Beam Search会考虑前 n 个最可能的标记,其中 n 代表集束的数量。这一过程会一直重复,直到达到预定义的最大长度或出现序列结束标记。此时,选择得分最高的序列(或“集束”)作为输出。
我们可以调整之前的函数,使其考虑概率最高的 n 个标记,而不仅仅是其中一个。在这里,我们将保持序列分数 $\log P(w)$ ,它是光束中每个标记对数概率的累积和。我们将此分数按序列长度进行归一化,以防止对较长的序列产生偏差(这个因子可以调整)。再次,我们将生成五个额外的token来完成句子“I have a dream”
from tqdm.notebook import tqdm
def greedy_sampling(logits, beams):
return torch.topk(logits, beams).indices
def beam_search(input_ids, node, bar, length, beams, sampling, temperature=0.1):
if length == 0:
return None
outputs = model(input_ids)
predictions = outputs.logits
# Get the predicted next sub-word (here we use top-k search)
logits = predictions[0, -1, :]
if sampling == 'greedy':
top_token_ids = greedy_sampling(logits, beams)
elif sampling == 'top_k':
top_token_ids = top_k_sampling(logits, temperature, 20, beams)
elif sampling == 'nucleus':
top_token_ids = nucleus_sampling(logits, temperature, 0.5, beams)
for j, token_id in enumerate(top_token_ids):
bar.update(1)
# Compute the score of the predicted token
token_score = get_log_prob(logits, token_id)
cumulative_score = graph.nodes[node]['cumscore'] + token_score
# Add the predicted token to the list of input ids
new_input_ids = torch.cat([input_ids, token_id.unsqueeze(0).unsqueeze(0)], dim=-1)
# Add node and edge to graph
token = tokenizer.decode(token_id, skip_special_tokens=True)
current_node = list(graph.successors(node))[j]
graph.nodes[current_node]['tokenscore'] = np.exp(token_score) * 100
graph.nodes[current_node]['cumscore'] = cumulative_score
graph.nodes[current_node]['sequencescore'] = 1/(len(new_input_ids.squeeze())) * cumulative_score
graph.nodes[current_node]['token'] = token + f"_{length}_{j}"
# Recursive call
beam_search(new_input_ids, current_node, bar, length-1, beams, sampling, 1)
# Parameters
length = 5
beams = 2
# Create a balanced tree with height 'length' and branching factor 'k'
graph = nx.balanced_tree(beams, length, create_using=nx.DiGraph())
bar = tqdm(total=len(graph.nodes))
# Add 'tokenscore', 'cumscore', and 'token' attributes to each node
for node in graph.nodes:
graph.nodes[node]['tokenscore'] = 100
graph.nodes[node]['cumscore'] = 0
graph.nodes[node]['sequencescore'] = 0
graph.nodes[node]['token'] = text
# Start generating text
beam_search(input_ids, 0, bar, length, beams, 'greedy', 1)
该函数计算了 63 个 token 和 beams^length = 2^5 = 32 种可能序列的分数。在我们的实现中,所有信息都存储在图中。我们的下一步是提取最佳序列。
首先,我们识别出具有最高序列分数的叶节点。接着,我们找到从根节点到该叶节点的最短路径。这条路径上的每个节点都包含最优序列中的一个标记。以下是我们如何实现它的方法:
def get_best_sequence(G):
# Create a list of leaf nodes
leaf_nodes = [node for node in G.nodes() if G.out_degree(node)==0]
# Get the leaf node with the highest cumscore
max_score_node = None
max_score = float('-inf')
for node in leaf_nodes:
if G.nodes[node]['sequencescore'] > max_score:
max_score = G.nodes[node]['sequencescore']
max_score_node = node
# Retrieve the sequence of nodes from this leaf node to the root node in a list
path = nx.shortest_path(G, source=0, target=max_score_node)
# Return the string of token attributes of this sequence
sequence = "".join([G.nodes[node]['token'].split('_')[0] for node in path])
return sequence, max_score
sequence, max_score = get_best_sequence(graph)
print(f"Generated text: {sequence}")
Generated text: I have a dream. I have a dream
在这个可视化中,我们将展示每个节点的序列分数,该分数代表到目前为止序列的得分。如果函数 get_best_sequence() 是正确的,那么在序列“I have a dream。I have a dream”中的“dream”节点,应该在所有叶节点中得分最高。
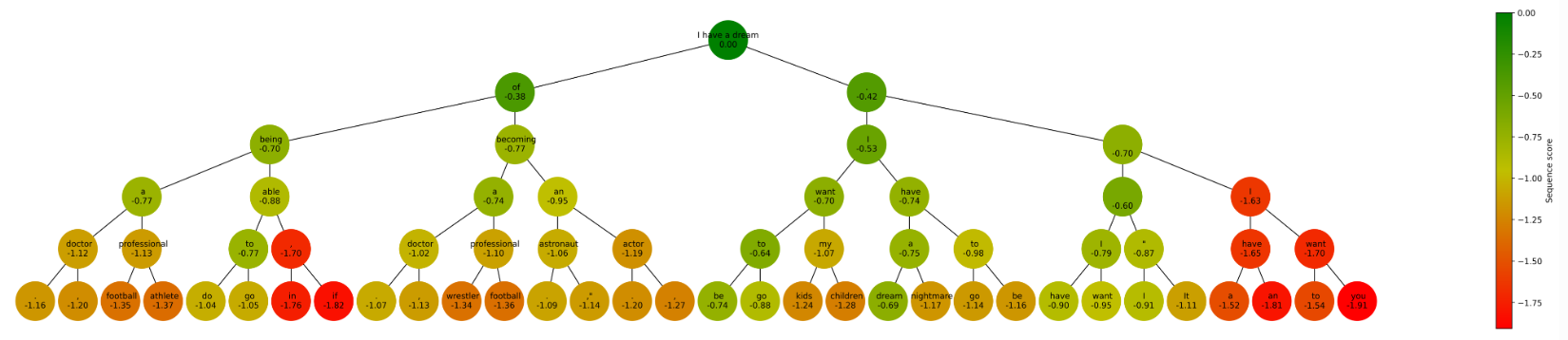
确实,“dream”这个 token 的序列得分最高,值为-0.69。有趣的是,我们可以看到左侧贪婪序列“I have a dream of being a doctor.”的得分为-1.16。
正如预期,贪婪搜索会导致次优结果。但坦白说,我们新的结果也不够吸引人。为了生成更多样化的序列,我们将实现两种采样算法:top-k 和 nucleus。
Top-k sampling
Top-k 采样是一种利用语言模型生成的概率分布,从最可能的 k 个选项中随机选择一个标记的技术。
假设我们有 k = 3 和四个标记:A、B、C 和 D,相应的概率分别为: P(A) = 30% 、 P(B) = 15% 、 P(C) = 5% 和 P(D) = 1% 。在 top-k 采样中,标记 D 被忽略,算法将 60% 的概率输出 A,30% 的概率输出 B,10% 的概率输出 C。这种方法确保了我们优先考虑最可能的标记,同时在选择过程中引入了随机性。
引入随机性的另一种方式是温度的概念。温度 T 是一个介于 0 到 1 之间的参数,它影响 softmax 函数生成的概率,使最可能的词更有影响力。在实践中,它仅仅是将输入 logits 除以一个我们称为温度的值:$\text{softmax}(x_i) = \frac{e^{x_i / T}}{\sum_{j} e^{x_j / T}}$
这里有一个图表,展示了温度对给定输入 logits [1.5, -1.8, 0.9, -3.2]生成的概率的影响。我们绘制了三个不同的温度值,以观察差异。
温度为 1.0 相当于没有温度的默认 softmax。另一方面,低温度设置(0.1)会显著改变概率分布。这通常用于文本生成,以控制生成输出的“创造性”水平。通过调整温度,我们可以影响模型产生更多样化或可预测响应的程度。
现在让我们实现 top k 采样算法。我们将通过提供“top_k”参数来在 beam_search() 函数中使用它。为了说明算法的工作原理,我们还将绘制 top_k=20 的概率分布图。
def plot_prob_distribution(probabilities, next_tokens, sampling, potential_nb, total_nb=50):
# Get top k tokens
top_k_prob, top_k_indices = torch.topk(probabilities, total_nb)
top_k_tokens = [tokenizer.decode([idx]) for idx in top_k_indices.tolist()]
# Get next tokens and their probabilities
next_tokens_list = [tokenizer.decode([idx]) for idx in next_tokens.tolist()]
next_token_prob = probabilities[next_tokens].tolist()
# Create figure
plt.figure(figsize=(0.4*total_nb, 5), dpi=300, facecolor='white')
plt.rc('axes', axisbelow=True)
plt.grid(axis='y', linestyle='-', alpha=0.5)
if potential_nb < total_nb:
plt.axvline(x=potential_nb-0.5, ls=':', color='grey', label='Sampled tokens')
plt.bar(top_k_tokens, top_k_prob.tolist(), color='blue')
plt.bar(next_tokens_list, next_token_prob, color='red', label='Selected tokens')
plt.xticks(rotation=45, ha='right', va='top')
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
if sampling == 'top_k':
plt.title('Probability distribution of predicted tokens with top-k sampling')
elif sampling == 'nucleus':
plt.title('Probability distribution of predicted tokens with nucleus sampling')
plt.legend()
plt.savefig(f'{sampling}_{time.time()}.png', dpi=300)
plt.close()
def top_k_sampling(logits, temperature, top_k, beams, plot=True):
assert top_k >= 1
assert beams <= top_k
indices_to_remove = logits < torch.topk(logits, top_k)[0][..., -1, None]
new_logits = torch.clone(logits)
new_logits[indices_to_remove] = float('-inf')
# Convert logits to probabilities
probabilities = torch.nn.functional.softmax(new_logits / temperature, dim=-1)
# Sample n tokens from the resulting distribution
next_tokens = torch.multinomial(probabilities, beams)
# Plot distribution
if plot:
total_prob = torch.nn.functional.softmax(logits / temperature, dim=-1)
plot_prob_distribution(total_prob, next_tokens, 'top_k', top_k)
return next_tokens
# Start generating text
beam_search(input_ids, 0, bar, length, beams, 'top_k', 1)
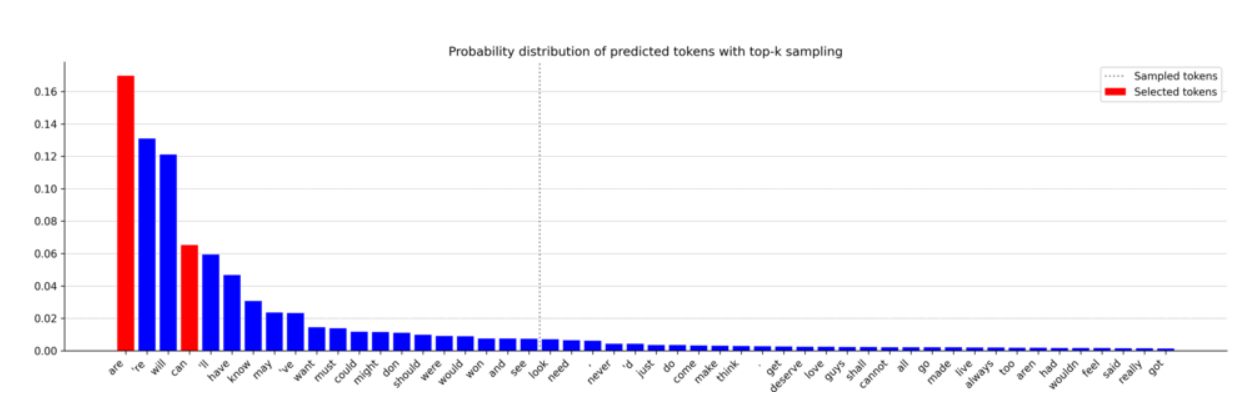
这些图表很好地展示了 top-k 采样是如何工作的,所有可能被选中的标记都位于水平条的左侧。虽然最可能的标记(红色)大部分时间被选中,但也允许不太可能的标记被选择。这提供了一个有趣的权衡,可以使序列倾向于一个不太可预测但听起来更自然的句子。现在让我们打印它生成的文本。
sequence, max_score = get_best_sequence(graph)
print(f"Generated text: {sequence}") # Generated text: I have a dream job and I want to
让我们看看这个决策树与上一个有何不同。
# Plot graph
plot_graph(graph, length, beams, 'sequence')
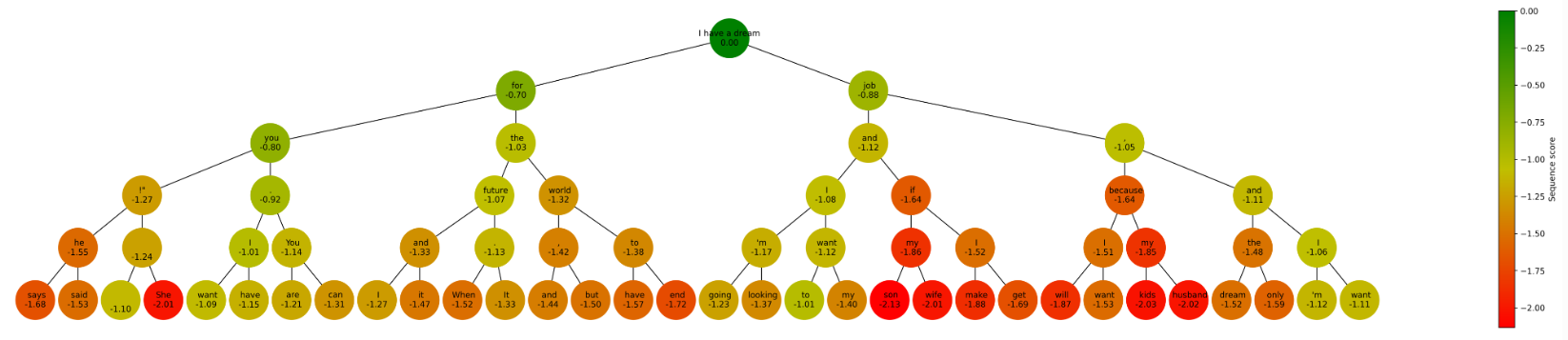
你可以看到这些节点与上一次迭代相比有显著差异,做出了更多样化的选择。尽管这个新结果的序列得分可能不是最高的(-1.01 而不是之前的-0.69),但重要的是要记住,更高的得分并不总是导致更真实或更有意义的序列。
现在我们已经介绍了 top-k 采样,接下来我们要介绍另一种最流行的采样技术:核采样。
Nucleus sampling
核采样,也称为 top-p 采样,与 top-k 采样采用了不同的方法。它不是选择概率最高的前 k 个 token,而是选择一个截止值 p ,使得所选 token 的概率之和超过 p 。这样就形成了一个“核”token 集合,从中随机选择下一个 token。
换句话说,模型按概率从高到低检查其 token,并将它们逐个添加到列表中,直到总概率超过阈值 p 。与 top-k 采样不同,核中包含的 token 数量每一步都可能不同。这种可变性通常能产生更多样化和富有创造力的输出,因此核采样在文本生成等任务中很受欢迎。
要实现核采样方法,我们可以使用 beam_search() 函数中的“核”参数。在这个例子中,我们将 p 的值设置为 0.5。为了简化,我们将包含一个最小数量的标记,等于束的数量。我们还将考虑累积概率低于 p 的标记,而不是高于。值得注意的是,虽然细节可能不同,但核采样的核心思想保持不变。
def nucleus_sampling(logits, temperature, p, beams, plot=True):
assert p > 0
assert p <= 1
# Sort the probabilities in descending order and compute cumulative probabilities
sorted_logits, sorted_indices = torch.sort(logits, descending=True)
probabilities = torch.nn.functional.softmax(sorted_logits / temperature, dim=-1)
cumulative_probabilities = torch.cumsum(probabilities, dim=-1)
# Create a mask for probabilities that are in the top-p
mask = cumulative_probabilities < p
# If there's not n index where cumulative_probabilities < p, we use the top n tokens instead
if mask.sum() > beams:
top_p_index_to_keep = torch.where(mask)[0][-1].detach().cpu().tolist()
else:
top_p_index_to_keep = beams
# Only keep top-p indices
indices_to_remove = sorted_indices[top_p_index_to_keep:]
sorted_logits[indices_to_remove] = float('-inf')
# Sample n tokens from the resulting distribution
probabilities = torch.nn.functional.softmax(sorted_logits / temperature, dim=-1)
next_tokens = torch.multinomial(probabilities, beams)
# Plot distribution
if plot:
total_prob = torch.nn.functional.softmax(logits / temperature, dim=-1)
plot_prob_distribution(total_prob, next_tokens, 'nucleus', top_p_index_to_keep)
return next_tokens
# Start generating text
beam_search(input_ids, 0, bar, length, beams, 'nucleus', 1)
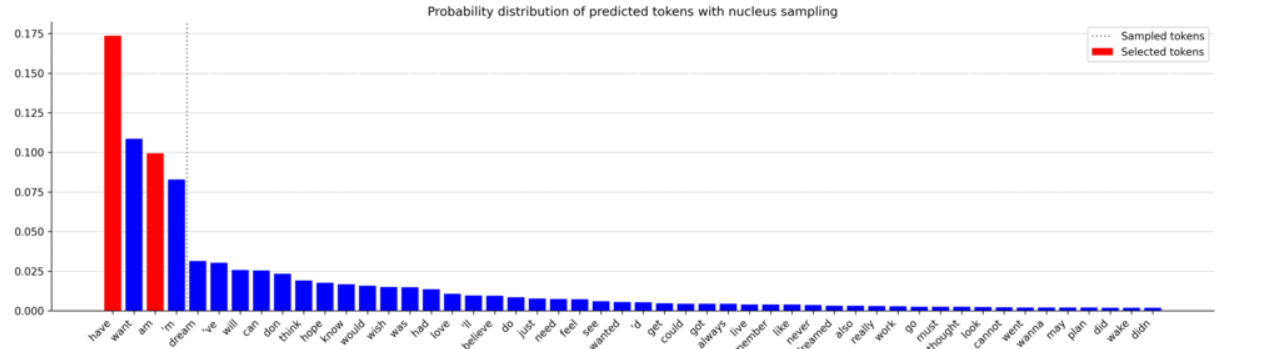
在这个图中,你可以看到核中包含的 token 数量波动很大。生成的概率分布差异显著,导致选择的 token 并不总是最有可能的。这为生成独特且多样的序列打开了大门。现在,让我们看看它生成的文本。
sequence, max_score = get_best_sequence(graph)
print(f"Generated text: {sequence}") # Generated text: I have a dream. I'm going to
要比较决策路径,让我们可视化新生成的树核采样。
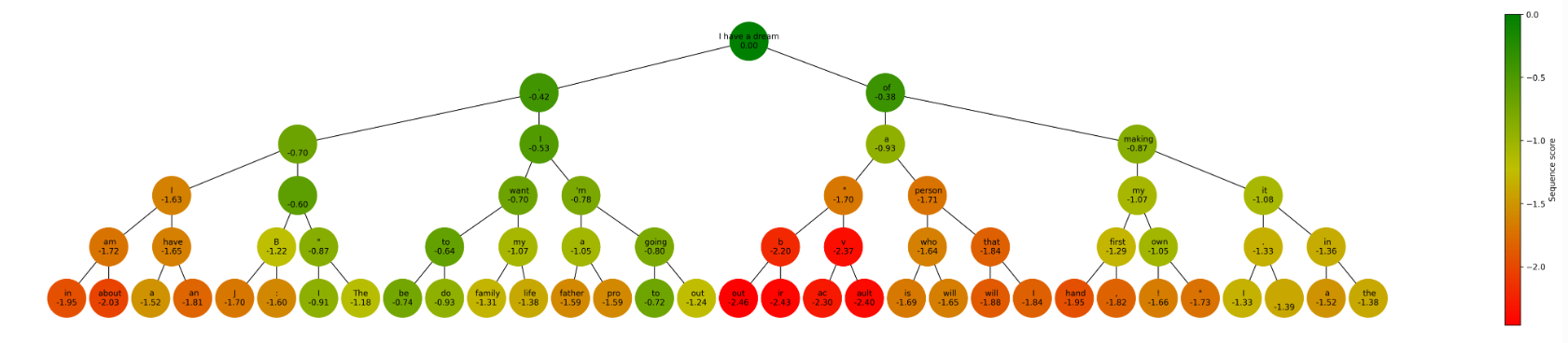
与 top-k 采样类似,这棵树与贪婪采样生成的树非常不同,显示出更多多样性。top-k 采样和核采样在生成文本时都提供了独特的优势,增强了多样性,并将创造力引入输出中。您在两种方法(甚至贪婪搜索)之间的选择将取决于您项目的具体需求和限制。
Conclusion
在这篇文章中,我们深入探讨了 LLMs(特别是 GPT-2)所使用的各种解码方法。我们从简单的贪婪搜索开始,它立即选择最可能的下一个标记,尽管这通常不是最优的。接下来,我们介绍了束搜索技术,它在每一步考虑多个最可能的标记。虽然束搜索能提供更细致的结果,但它有时在生成多样化和富有创造性的序列方面会显得不足。
为了使过程更具多样性,我们随后介绍了 top-k 采样和核采样。top-k 采样通过随机选择 k 个最可能的标记来使文本生成多样化,而核采样则通过根据累积概率动态形成标记核来采取不同的路径。这些方法各自具有独特的优势和潜在缺点,而你的项目的具体需求将主要决定在这些方法之间的选择。