数学运算技巧

一行代码解决的算法题

能够通过一行代码解决的算法题一定是脑筋急转弯，通过想出规律，直接解决

这里就要提到规律是怎么想出来的。其实人是可以学习计算机枚举思维的，通过枚举一些简单的栗子，就能够摸到一点规律了

Nim游戏

题目

你和你的朋友面前有一堆石子，你们轮流拿，一次至少拿一颗，最多拿三颗，谁拿走最后一颗石子谁获胜。

假设你们都很聪明，由你第一个开始拿，请你写一个算法，输入一个正整数 n，返回你是否能赢（true 或 false）。

思路

比如现在有 4 颗石子，算法应该返回 false。因为无论你拿 1 颗 2 颗还是 3 颗，对方都能一次性拿完，拿走最后一颗石子，所以你一定会输。

首先，这道题肯定可以使用动态规划，因为显然原问题存在子问题，且子问题存在重复。但是因为你们都很聪明，涉及到你和对手的博弈，动态规划会比较复杂。

我们解决这种问题的思路一般都是反着思考：

如果我能赢，那么最后轮到我取石子的时候必须要剩下 1~3 颗石子，这样我才能一把拿完。

如何营造这样的一个局面呢？显然，如果对手拿的时候只剩 4 颗石子，那么无论他怎么拿，总会剩下 1~3 颗石子，我就能赢。

如何逼迫对手面对 4 颗石子呢？要想办法，让我选择的时候还有 5~7 颗石子，这样的话我就有把握让对方不得不面对 4 颗石子。

如何营造 5~7 颗石子的局面呢？让对手面对 8 颗石子，无论他怎么拿，都会给我剩下 5~7 颗，我就能赢。

这样一直循环下去，我们发现只要踩到 4 的倍数，就落入了圈套，永远逃不出 4 的倍数，而且一定会输。所以这道题的解法非常简单：

bool canWinNim(int n) {
    // 如果上来就踩到 4 的倍数，那就认输吧
    // 否则，可以把对方控制在 4 的倍数，必胜
    return n % 4 != 0;
}

石头游戏

题目

你和你的朋友面前有一排石头堆，用一个数组 piles 表示，piles[i] 表示第 i 堆石子有多少个。你们轮流拿石头，一次拿一堆，但是只能拿走最左边或者最右边的石头堆。所有石头被拿完后，谁拥有的石头多，谁获胜。

假设你们都很聪明，由你第一个开始拿，请你写一个算法，输入一个数组 piles，返回你是否能赢（true 或 false）。

注意，石头的堆的数量为偶数，所以你们两人拿走的堆数一定是相同的。石头的总数为奇数，也就是你们最后不可能拥有相同多的石头，一定有胜负之分。

思路

举个例子，piles=[2, 1, 9, 5]，你先拿，可以拿 2 或者 5，你选择 2。

piles=[1, 9, 5]，轮到对手，可以拿 1 或 5，他选择 5。

piles=[1, 9] 轮到你拿，你拿 9。

最后，你的对手只能拿 1 了。

这样下来，你总共拥有 2 + 9 = 11 颗石头，对手有 5 + 1 = 6 颗石头，你是可以赢的，所以算法应该返回 true。

你看到了，并不是简单的挑数字大的选，为什么第一次选择 2 而不是 5 呢？因为 5 后面是 9，你要是贪图一时的利益，就把 9 这堆石头暴露给对手了，那你就要输了。

这也是强调双方都很聪明的原因，算法也是求最优决策过程下你是否能赢。

这道题又涉及到两人的博弈，也可以用动态规划算法暴力试，比较麻烦。但我们只要对规则深入思考，就会大惊失色：只要你足够聪明，你是必胜无疑的，因为你是先手。

bool stoneGame(vector<int>& piles) {
    return true;
}

这是为什么呢，因为题目有两个条件很重要：一是石头总共有偶数堆，石头的总数是奇数。这两个看似增加游戏公平性的条件，反而使该游戏成为了一个割韭菜游戏。我们以 piles=[2, 1, 9, 5] 讲解，假设这四堆石头从左到右的索引分别是 1，2，3，4。

如果我们把这四堆石头按索引的奇偶分为两组，即第 1、3 堆和第 2、4 堆，那么这两组石头的数量一定不同，也就是说一堆多一堆少。因为石头的总数是奇数，不能被平分。

而作为第一个拿石头的人，你可以控制自己拿到所有偶数堆，或者所有的奇数堆。

你最开始可以选择第 1 堆或第 4 堆。如果你想要偶数堆，你就拿第 4 堆，这样留给对手的选择只有第 1、3 堆，他不管怎么拿，第 2 堆又会暴露出来，你就可以拿。同理，如果你想拿奇数堆，你就拿第 1 堆，留给对手的只有第 2、4 堆，他不管怎么拿，第 3 堆又给你暴露出来了。

也就是说，你可以在第一步就观察好，奇数堆的石头总数多，还是偶数堆的石头总数多，然后步步为营，就一切尽在掌控之中了。知道了这个漏洞，可以整一整不知情的同学了。

电灯开关问题

题目

有 n 盏电灯，最开始时都是关着的。现在要进行 n 轮操作：

第 1 轮操作是把每一盏电灯的开关按一下（全部打开）。

第 2 轮操作是把每两盏灯的开关按一下（就是按第 2，4，6… 盏灯的开关，它们被关闭）。

第 3 轮操作是把每三盏灯的开关按一下（就是按第 3，6，9… 盏灯的开关，有的被关闭，比如 3，有的被打开，比如 6）…

如此往复，直到第 n 轮，即只按一下第 n 盏灯的开关。

现在给你输入一个正整数 n 代表电灯的个数，问你经过 n 轮操作后，这些电灯有多少盏是亮的？

思路

我们当然可以用一个布尔数组表示这些灯的开关情况，然后模拟这些操作过程，最后去数一下就能出结果。但是这样显得没有灵性，最好的解法是这样的：

int bulbSwitch(int n) {
    return (int)sqrt(n);
}

首先，因为电灯一开始都是关闭的，所以某一盏灯最后如果是点亮的，必然要被按奇数次开关。

我们假设只有 6 盏灯，而且我们只看第 6 盏灯。需要进行 6 轮操作对吧，请问对于第 6 盏灯，会被按下几次开关呢？这不难得出，第 1 轮会被按，第 2 轮，第 3 轮，第 6 轮都会被按。

为什么第 1、2、3、6 轮会被按呢？因为 6=1*6=2*3。一般情况下，因子都是成对出现的，也就是说开关被按的次数一般是偶数次。但是有特殊情况，比如说总共有 16 盏灯，那么第 16 盏灯会被按几次?16 = 1*16 = 2*8 = 4*4

其中因子 4 重复出现，所以第 16 盏灯会被按 5 次，奇数次。现在你应该理解这个问题为什么和平方根有关了吧？

不过，我们不是要算最后有几盏灯亮着吗，这样直接平方根一下是啥意思呢？稍微思考一下就能理解了。

就假设现在总共有 16 盏灯，我们求 16 的平方根，等于 4，这就说明最后会有 4 盏灯亮着，它们分别是第 1*1=1 盏、第 2*2=4 盏、第 3*3=9 盏和第 4*4=16 盏。

就算有的 n 平方根结果是小数，强转成 int 型，也相当于一个最大整数上界，比这个上界小的所有整数，平方后的索引都是最后亮着的灯的索引。所以说我们直接把平方根转成整数，就是这个问题的答案。

反直觉的概率问题

计算概率有下面两个最简单的原则：

原则一、计算概率一定要有一个参照系，称作「样本空间」，即随机事件可能出现的所有结果。事件 A 发生的概率 = A 包含的样本点 / 样本空间的样本总数。

原则二、计算概率一定要明白，概率是一个连续的整体，不可以把连续的概率分割开，也就是所谓的条件概率。

上述两个原则高中就学过，但是我们还是很容易犯错，而且犯错的流程也有异曲同工之妙：

先是忽略了原则二，错误地计算了样本空间，然后通过原则一算出了错误的答案。

男孩女孩问题

假设有一个家庭，有两个孩子，现在告诉你其中有一个男孩，请问另一个也是男孩的概率是多少？

不假思索地回答：1/2 啊，因为另一个孩子要么是男孩，要么是女孩，而且概率相等呀。但是实际上，答案是 1/3。

上述思想为什么错误呢？因为没有正确计算样本空间，导致原则一计算错误。有两个孩子，那么样本空间为 4，即哥哥妹妹，哥哥弟弟，姐姐妹妹，姐姐弟弟这四种情况。已知有一个男孩，那么排除姐姐妹妹这种情况，所以样本空间变成 3。另一个孩子也是男孩只有哥哥弟弟这 1 种情况，所以概率为 1/3。

为什么计算样本空间会出错呢？因为我们忽略了条件概率，即混淆了下面两个问题：

这个家庭只有一个孩子，这个孩子是男孩的概率是多少？

这个家庭有两个孩子，其中一个是男孩，另一个孩子是男孩的概率是多少？

根据原则二，概率问题是连续的，不可以把上述两个问题混淆。第二个问题需要用条件概率，即求一个孩子是男孩的条件下，另一个也是男孩的概率。运用条件概率的公式也很好算，就不多说了。

通过这个问题，读者应该理解两个概率计算原则的关系了，最具有迷惑性的就是条件概率的忽视。为了不要被迷惑，最简单的办法就是把所有可能结果穷举出来。

最后，对于此问题我见过一个很奇葩的质疑：如果这两个孩子是双胞胎，不存在年龄上的差异怎么办？

有那么一丝道理！但其实，我们只是通过年龄差异来表示两个孩子的独立性，也就是说即便两个孩子同性，也有两种可能。所以不要用双胞胎抬杠了。

生日悖论

生日悖论是由这样一个问题引出的：一个屋子里需要有多少人，才能使得存在至少两个人生日是同一天的概率达到 50%？

答案是 23 个人，也就是说房子里如果有 23 个人，那么就有 50% 的概率会存在两个人生日相同。这个结论看起来不可思议，所以被称为悖论。按照直觉，要得到 50% 的概率，起码得有 183 个人吧，因为一年有 365 天呀？其实不是的，觉得这个结论不可思议主要有两个思维误区：

第一个误区是误解「存在」这个词的含义。

读者可能认为，如果 23 个人中出现相同生日的概率就能达到 50%，是不是意味着：

假设现在屋子里坐着 22 个人，然后我走进去，那么有 50% 的概率我可以找到一个人和我生日相同。但这怎么可能呢？

并不是的，你这种想法是以自我为中心，而题目的概率是在描述整体。也就是说「存在」的含义是指 23 人中的任意两个人，涉及排列组合，大概率和你没啥关系。

如果你非要计算存在和自己生日相同的人的概率是多少，可以这样计算：

1 - P(22 个人都和我的生日不同) = 1 -(364/365)^22 = 0.06

这样计算得到的结果是不是看起来合理多了？生日悖论计算对象的不是某一个人，而是一个整体，其中包含了所有人的排列组合，它们的概率之和当然会大得多。

第二个误区是认为概率是线性变化的。

读者可能认为，如果 23 个人中出现相同生日的概率就能达到 50%，是不是意味着 46 个人的概率就能达到 100%？

不是的，就像中奖率 50% 的游戏，你玩两次的中奖率就是 100% 吗？显然不是，你玩两次的中奖率是 75%：

P(两次能中奖) = P(第一次就中了) + P(第一次没中但第二次中了) = 1/2 + 1/2*1/2 = 75%

那么换到生日悖论也是一个道理，概率不是简单叠加，而要考虑一个连续的过程，所以这个结论并没有什么不合常理之处。

那为什么只要 23 个人出现相同生日的概率就能大于 50% 了呢？我们先计算 23 个人生日都唯一（不重复）的概率。只有 1 个人的时候，生日唯一的概率是 365/365，2 个人时，生日唯一的概率是 365/365 × 364/365，以此类推可知 23 人的生日都唯一的概率：

算出来大约是 0.493，所以存在相同生日的概率就是 0.507，差不多就是 50% 了。实际上，按照这个算法，当人数达到 70 时，存在两个人生日相同的概率就上升到了 99.9%，基本可以认为是 100% 了。所以从概率上说，一个几十人的小团体中存在生日相同的人真没啥稀奇的。

三门问题

这个游戏很经典了：游戏参与者面对三扇门，其中两扇门后面是山羊，一扇门后面是跑车。参与者只要随便选一扇门，门后面的东西就归他（跑车的价值当然更大）。但是主持人决定帮一下参与者：在他选择之后，先不急着打开这扇门，而是由主持人打开剩下两扇门中的一扇，展示其中的山羊（主持人知道每扇门后面是什么），然后给参与者一次换门的机会，此时参与者应该换门还是不换门呢？

为了防止第一次看到这个问题的读者迷惑，再具体描述一下这个问题：

你是游戏参与者，现在有门 1,2,3，假设你随机选择了门 1，然后主持人打开了门 3 告诉你那后面是山羊。现在，你是坚持你最初的选择门 1，还是选择换成门 2 呢？

答案是应该换门，换门之后抽到跑车的概率是 2/3，不换的话是 1/3。又一次反直觉，感觉换不换的中奖概率应该都一样啊，因为最后肯定就剩两个门，一个是羊，一个是跑车，这是事实，所以不管选哪个的概率不都是 1/2 吗？

类似前面说的男孩女孩问题，最简单稳妥的方法就是把所有可能结果穷举出来：

很容易看到选择换门中奖的概率是 2/3，不换的话是 1/3。

关于这个问题还有更简单的方法：主持人开门实际上在「浓缩」概率。一开始你选择到跑车的概率当然是 1/3，剩下两个门中包含跑车的概率当然是 2/3，这没啥可说的。但是主持人帮你排除了一个含有山羊的门，相当于把那 2/3 的概率浓缩到了剩下的这一扇门上。那么，你说你是抱着原来那扇 1/3 的门，还是换成那扇经过「浓缩」的 2/3 概率的门呢？

再直观一点，假设你三选一，剩下 2 扇门，再给你加入 98 扇装山羊的门，把这 100 扇门随机打乱，问你换不换？肯定不换对吧，这明摆着把概率稀释了，肯定抱着原来的那扇门是最可能中跑车的。再假设，初始有 100 扇门，你选了一扇，然后主持人在剩下 99 扇门中帮你排除 98 个山羊，问你换不换一扇门？肯定换对吧，你手上那扇门是 1%，另一扇门是 99%，或者也可以这样理解，不换只是选择了 1 扇门，换门相当于选择了 99 扇门，这样结果很明显了吧？

以上思想，也许有的读者都思考过，下面我们思考这样一个问题：假设你在决定是否换门的时候，小明破门而入，要求帮你做出选择。他完全不知道之前发生的事，他只知道面前有两扇门，一扇是跑车一扇是山羊，那么他抽中跑车的概率是多大？

当然是 1/2，这也是很多人做错三门问题的根本原因。类似生日悖论，人们总是容易以自我为中心，通过这个小明的视角来计算是否换门，这显然会进入误区。

就好比有两个箱子，一号箱子有 4 个黑球 2 个红球，二号箱子有 2 个黑球 4 个红球，随便选一个箱子，随便摸一个球，问你摸出红球的概率。

对于不知情的小明，他会随机选择一个箱子，随机摸球，摸到红球的概率是：1/2 × 2/6 + 1/2 × 4/6 = 1/2

对于知情的你，你知道在二号箱子摸球概率大，所以只在二号箱摸，摸到红球的概率是：0 × 2/6 + 1 × 4/6 = 2/3

三门问题是有指导意义的。比如你蒙选择题，先蒙了 A，后来灵机一动排除了 B 和 C，请问你是否要把 A 换成 D？答案是，换！

也许读者会问，如果只排除了一个答案，比如说 B，那么我是否应该把 A 换成 C 或者 D 呢？答案是，换！

因为按照刚才「浓缩」概率这个思想，只要进行了排除，都是在进行「浓缩」，均摊下来肯定比你一开始蒙的那个答案概率 1/4 高。比如刚才的例子，C 和 D 的正确概率都是 3/8，而你开始蒙的 A 只有 1/4。

常用位操作

几个有趣的位操作

利用或操作 | 和空格将英文字符转换为小写

('a' | ' ') = 'a'
('A' | ' ') = 'a'

利用与操作 & 和下划线将英文字符转换为大写

('b' & '_') = 'B'
('B' & '_') = 'B'

利用异或操作 ^ 和空格进行英文字符大小写互换

('d' ^ ' ') = 'D'
('D' ^ ' ') = 'd'

以上操作能够产生奇特效果的原因在于 ASCII 编码。ASCII 字符其实就是数字，恰巧空格和下划线对应的数字通过位运算就能改变大小写。有兴趣的读者可以查 ASCII 码表自己算算，本文就不展开讲了。

不用临时变量交换两个数

int a = 1, b = 2;
a ^= b;
b ^= a;
a ^= b;
// 现在 a = 2, b = 1

加一

int n = 1;
n = -~n;
// 现在 n = 2

减一

int n = 2;
n = ~-n;
// 现在 n = 1

判断两个数是否异号

int x = -1, y = 2;
boolean f = ((x ^ y) < 0); // true

int x = 3, y = 2;
boolean f = ((x ^ y) < 0); // false

如果说前 6 个技巧的用处不大，这第 7 个技巧还是比较实用的，利用的是补码编码的符号位。整数编码最高位是符号位，负数的符号位是 1，非负数的符号位是 0，再借助异或的特性，可以判断出两个数字是否异号。

当然，如果不用位运算来判断是否异号，需要使用 if else 分支，还挺麻烦的。你可能想利用乘积来判断两个数是否异号，但是这种处理方式容易造成整型溢出，从而出现错误。

index & (arr.size() - 1)的运用

利用求模（余数）的方式让数组看起来头尾相接形成一个环形，永远都走不完：

#include <iostream>
using namespace std;

int main() {
    int arr[] = {1, 2, 3, 4};
    int index = 0;
    while (true) {
        // 绕着循环数组走
        cout << arr[index % (sizeof(arr) / sizeof(int))] << endl;
        index++;
    }
    // 无法到达的代码
    return 0;
}
// 输出：1,2,3,4,1,2,3,4,1,2,3,4...

但模运算 % 对计算机来说其实是一个比较昂贵的操作，所以我们可以用 & 运算来求余数：

int arr[] = {1,2,3,4};
int index = 0;
while (true) {
    // 在环形数组中转圈
    printf("%d ", arr[index & (sizeof(arr)/sizeof(arr[0]) - 1)]);
    index++;
}
// 输出：1,2,3,4,1,2,3,4,1,2,3,4...
// 注意这个技巧只适用于数组长度是 2 的幂次方的情况，比如 2、4、8、16、32 以此类推。

简单说，& (arr.length - 1) 这个位运算能够替代 % arr.length 的模运算，性能会更好一些。

那问题来了，现在是不断地 index++，你做到了循环遍历。但如果不断地 index--，还能做到环形数组的效果吗？

答案是，如果你使用 % 求模的方式，那么当 index 小于 0 之后求模的结果也会出现负数，你需要特殊处理。但通过 & 与运算的方式，index 不会出现负数，依然可以正常工作：

int arr[] = {1,2,3,4};
int index = 0;
while (true) {
    // 在环形数组中转圈
    cout << arr[index & (sizeof(arr) / sizeof(*arr) - 1)] << " ";
    index--;
}
// 输出：1,4,3,2,1,4,3,2,1,4,3,2,1...

n & (n - 1)的运用

n & (n-1) 这个操作在算法中比较常见，作用是消除数字 n 的二进制表示中的最后一个 1。

看个图就很容易理解了：

其核心逻辑就是，n - 1 一定可以消除最后一个 1，同时把其后的 0 都变成 1，这样再和 n 做一次 & 运算，就可以仅仅把最后一个 1 变成 0 了。

计算汉明权重

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为[汉明重量]）。

示例 1：

输入：n = 00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

示例 2：

输入：n = 00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。

示例 3：

输入：n = 11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。

提示：

• 输入必须是长度为 32 的 二进制串 。

进阶：

• 如果多次调用这个函数，你将如何优化你的算法？

因为 n & (n - 1) 可以消除最后一个 1，所以可以用一个循环不停地消除 1 同时计数，直到 n 变成 0 为止。

int hammingWeight(int n) {
    int res = 0;
    while (n != 0) {
        n = n & (n - 1);
        res++;
    }
    return res;
}

判断一个数是不是2的指数

一个数如果是 2 的指数，那么它的二进制表示一定只含有一个 1：

2^0 = 1 = 0b0001
2^1 = 2 = 0b0010
2^2 = 4 = 0b0100

如果使用 n & (n-1) 的技巧就很简单了（注意运算符优先级，括号不可以省略）：

bool isPowerOfTwo(int n) {
    if (n <= 0) return false;
    return (n & (n - 1)) == 0;
}

a ^ a = 0的运用

一个数和它本身做异或运算结果为 0，即 a ^ a = 0；一个数和 0 做异或运算的结果为它本身，即 a ^ 0 = a。

查找只出现一次的元素

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

示例 1 ：

输入：nums = [2,2,1]
输出：1

示例 2 ：

输入：nums = [4,1,2,1,2]
输出：4

示例 3 ：

输入：nums = [1]
输出：1

提示：

• 1 <= nums.length <= 3 * 104
• -3 * 104 <= nums[i] <= 3 * 104
• 除了某个元素只出现一次以外，其余每个元素均出现两次。

对于这道题目，我们只要把所有数字进行异或，成对儿的数字就会变成 0，落单的数字和 0 做异或还是它本身，所以最后异或的结果就是只出现一次的元素：

int singleNumber(vector<int>& nums) {
    int res = 0;
    for (int n : nums) {
        res ^= n;
    }
    return res;
}

寻找缺失的元素

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

示例 1：

输入：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 2：

输入：nums = [0,1]
输出：2
解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 3：

输入：nums = [9,6,4,2,3,5,7,0,1]
输出：8
解释：n = 9，因为有 9 个数字，所以所有的数字都在范围 [0,9] 内。8 是丢失的数字，因为它没有出现在 nums 中。

示例 4：

输入：nums = [0]
输出：1
解释：n = 1，因为有 1 个数字，所以所有的数字都在范围 [0,1] 内。1 是丢失的数字，因为它没有出现在 nums 中。

提示：

• n == nums.length
• 1 <= n <= 104
• 0 <= nums[i] <= n
• nums 中的所有数字都 独一无二

进阶：你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?

给一个长度为 n 的数组，其索引应该在 [0,n)，但是现在你要装进去 n + 1 个元素 [0,n]，那么肯定有一个元素装不下嘛，请你找出这个缺失的元素。

这道题不难的，我们应该很容易想到，把这个数组排个序，然后遍历一遍，不就很容易找到缺失的那个元素了吗？

或者说，借助数据结构的特性，用一个 HashSet 把数组里出现的数字都储存下来，再遍历 [0,n] 之间的数字，去 HashSet 中查询，也可以很容易查出那个缺失的元素。

排序解法的时间复杂度是 O(NlogN)，HashSet 的解法时间复杂度是 O(N)，但是还需要 O(N) 的空间复杂度存储 HashSet。

这个问题其实还有一个特别简单的解法：等差数列求和公式。

题目的意思可以这样理解：现在有个等差数列 0, 1, 2,..., n，其中少了某一个数字，请你把它找出来。那这个数字不就是 sum(0,1,..n) - sum(nums) 嘛？

int missingNumber(vector<int>& nums) {
    int n = nums.size();
    // 虽然题目给的数据范围不大，但严谨起见，用 long 类型防止整型溢出
    // 求和公式：(首项 + 末项) * 项数 / 2
    long expect = (0 + n) * (n + 1) / 2;
    long sum = 0;
    for (int x : nums) {
        sum += x;
    }
    return (int)(expect - sum);
}

不过，本文的主题是位运算，我们来讲讲如何利用位运算技巧来解决这道题。

异或运算满足交换律和结合律，也就是说：

2 ^ 3 ^ 2 = 3 ^ (2 ^ 2) = 3 ^ 0 = 3

而这道题索就可以通过这些性质巧妙算出缺失的那个元素，比如说 nums = [0,3,1,4]：

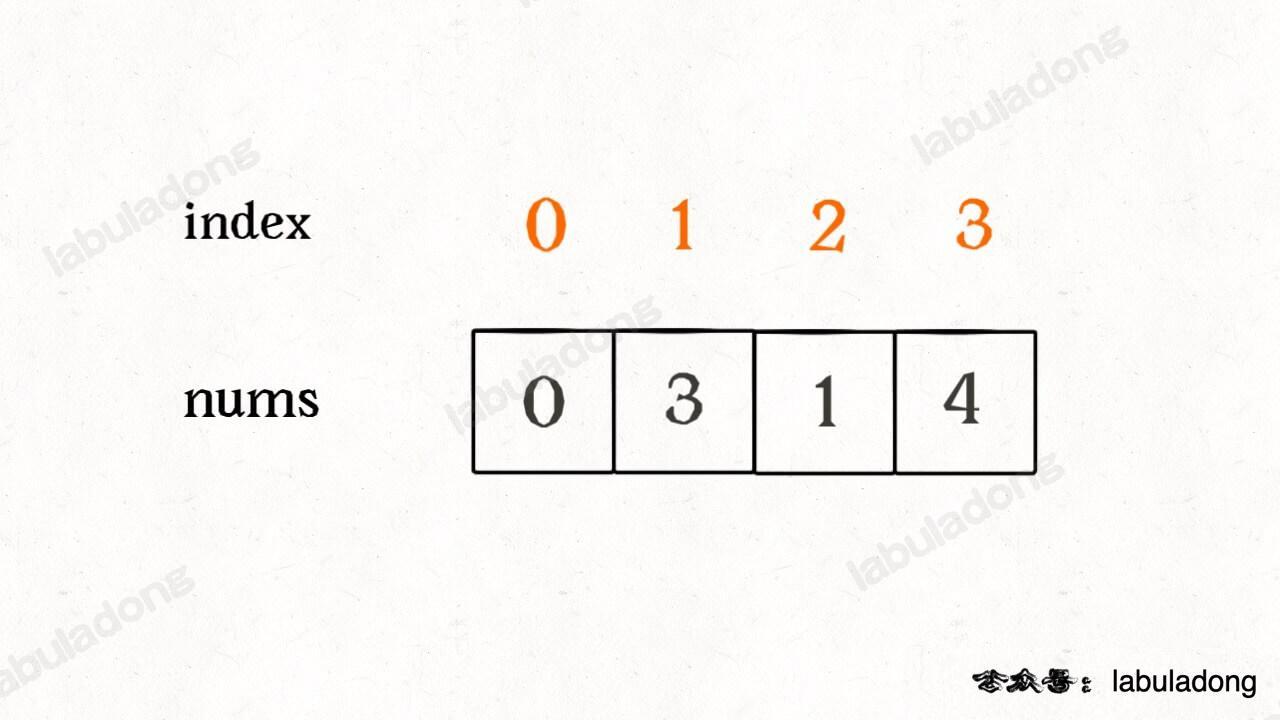
为了容易理解，我们假设先把索引补一位，然后让每个元素和自己相等的索引相对应：

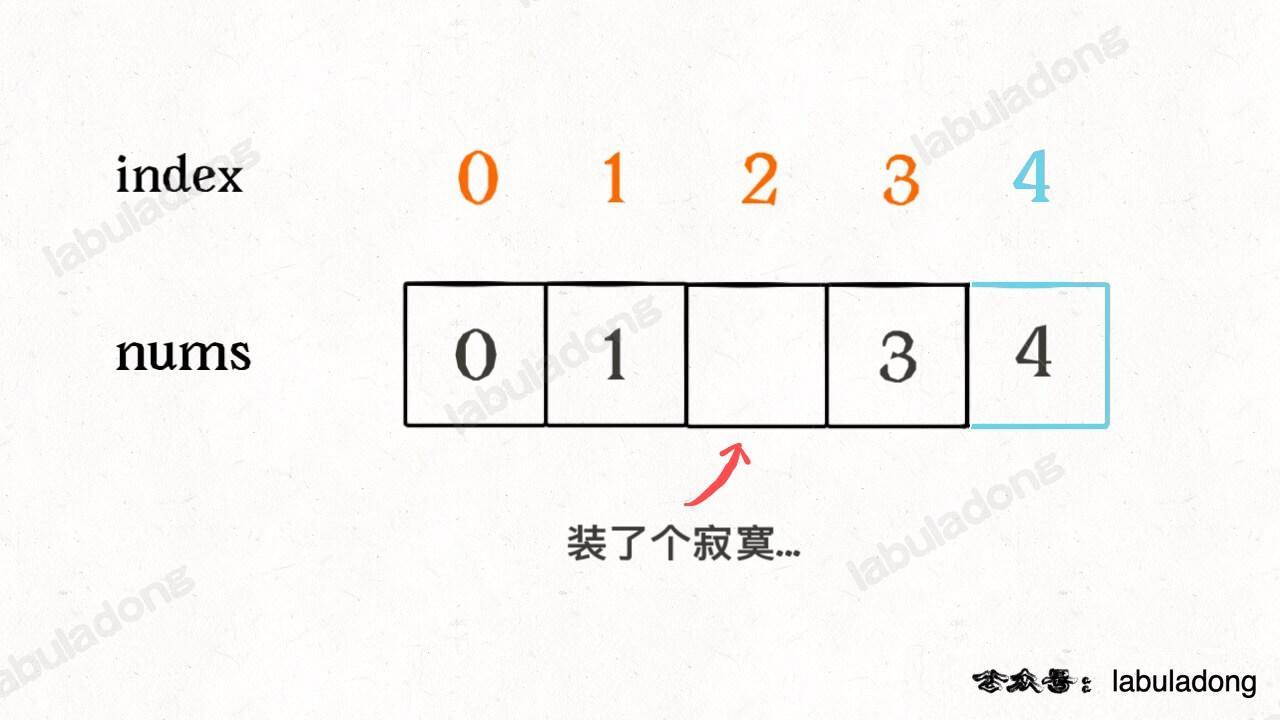
这样做了之后，就可以发现除了缺失元素之外，所有的索引和元素都组成一对儿了，现在如果把这个落单的索引 2 找出来，也就找到了缺失的那个元素。

如何找这个落单的数字呢，只要把所有的元素和索引做异或运算，成对儿的数字都会消为 0，只有这个落单的元素会剩下，也就达到了我们的目的：

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int n = nums.size();
        int res = 0;
        // 先和新补的索引异或一下
        res ^= n;
        // 和其他的元素、索引做异或
        for (int i = 0; i < n; i++)
            res ^= i ^ nums[i];
        return res;
    }
};

高效寻找素数

// 返回区间 [2, n) 中有几个素数 
int countPrimes(int n);

// 比如 countPrimes(10) 返回 4
// 因为 2,3,5,7 是素数

暴力硬算

int countPrimes(int n) {
    int count = 0;
    for (int i = 2; i < n; i++)
        if (isPrime(i)) count++;
    return count;
}

// 判断整数 n 是否是素数
bool isPrime(int n) {
    for (int i = 2; i < n; i++)
        if (n % i == 0)
            // 有其他整除因子
            return false;
    return true;
}

这样写的话时间复杂度 O(n^2)，问题很大。首先你用 isPrime 函数来辅助的思路就不够高效；而且就算你要用 isPrime 函数，这样写算法也是存在计算冗余的。

先来简单说下如果你要判断一个数是不是素数，应该如何写算法。只需稍微修改一下上面的 isPrime 代码中的 for 循环条件：

boolean isPrime(int n) {
    for (int i = 2; i * i <= n; i++)
        ...
}

换句话说，i 不需要遍历到 n，而只需要到 sqrt(n) 即可。为什么呢，我们举个例子，假设 n = 12。

12 = 2 × 6
12 = 3 × 4
12 = sqrt(12) × sqrt(12)
12 = 4 × 3
12 = 6 × 2

可以看到，后两个乘积就是前面两个反过来，反转临界点就在 sqrt(n)。

换句话说，如果在 [2,sqrt(n)] 这个区间之内没有发现可整除因子，就可以直接断定 n 是素数了，因为在区间 [sqrt(n),n] 也一定不会发现可整除因子。

现在，isPrime 函数的时间复杂度降为 O(sqrt(N))，但是我们实现 countPrimes 函数其实并不需要这个函数，以上只是希望读者明白 sqrt(n) 的含义，因为等会还会用到。

质筛法

素数筛选法的核心思路是和上面的常规思路反着来：

首先从 2 开始，我们知道 2 是一个素数，那么 2 × 2 = 4, 3 × 2 = 6, 4 × 2 = 8… 都不可能是素数了。

然后我们发现 3 也是素数，那么 3 × 2 = 6, 3 × 3 = 9, 3 × 4 = 12… 也都不可能是素数了。

Wikipedia 的这个 GIF 很形象：

先看我们的第一版代码：

int countPrimes(int n) {
    bool isPrime[n];
    // 将数组都初始化为 true
    memset(isPrime, true, sizeof(isPrime));

    for (int i = 2; i < n; i++) 
        if (isPrime[i]) 
            // i 的倍数不可能是素数了
            for (int j = 2 * i; j < n; j += i) 
                isPrime[j] = false;
    
    int count = 0;
    for (int i = 2; i < n; i++)
        if (isPrime[i]) count++;
    
    return count;
}

如果上面这段代码你能够理解，那么你已经掌握了整体思路，但是还有两个细微的地方可以优化。

首先，回想刚才判断一个数是否是素数的 isPrime 函数，由于因子的对称性，其中的 for 循环只需要遍历 [2,sqrt(n)] 就够了。这里也是类似的，我们外层的 for 循环也只需要遍历到 sqrt(n)：

for (int i = 2; i * i < n; i++) 
    if (isPrime[i]) 
        ...

除此之外，很难注意到内层的 for 循环也可以优化。我们之前的做法是：

for (int j = 2 * i; j < n; j += i) 
    isPrime[j] = false;

这样可以把 i 的整数倍都标记为 false，但是仍然存在计算冗余。

比如 n = 25，i = 5 时算法会标记 5 × 2 = 10，5 × 3 = 15 等等数字，但是这两个数字已经被 i = 2 和 i = 3 的 2 × 5 和 3 × 5 标记了。

我们可以稍微优化一下，让 j 从 i 的平方开始遍历，而不是从 2 * i 开始：

for (int j = i * i; j < n; j += i) 
    isPrime[j] = false;

这样，素数计数的算法就高效实现了，其实这个算法有一个名字，叫做 Sieve of Eratosthenes。看下完整的最终代码：

class Solution {
public:
    int countPrimes(int n) {
        vector<bool> isPrime(n, true);
        for (int i = 2; i * i < n; i++) {
            if (isPrime[i]) {
                for (int j = i * i; j < n; j += i) {
                    isPrime[j] = false;
                }
            }
        }
        
        int count = 0;
        for (int i = 2; i < n; i++) {
            if (isPrime[i]) {
                count++;
            }
        }
        
        return count;
    }
};

该算法的时间复杂度比较难算，显然时间跟这两个嵌套的 for 循环有关，其操作数应该是：

n/2 + n/3 + n/5 + n/7 + … = n × (1/2 + 1/3 + 1/5 + 1/7…)

括号中是素数的倒数。其最终结果是 O(N * loglogN)。

经典面试题

一文秒杀所有丑数系列问题

丑数I

题目

给你输入一个数字 n，请你判断 n 是否为「丑数」。所谓「丑数」，就是只包含质因数 2、3 和 5 的正整数。

函数签名如下：

bool isUgly(int n)

思路

比如 12 = 2 x 2 x 3 就是一个丑数，而 42 = 2 x 3 x 7 就不是一个丑数。

这道题其实非常简单，前提是你知道算术基本定理（正整数唯一分解定理）：

任意一个大于 1 的自然数，要么它本身就是质数，要么它可以分解为若干质数的乘积。

既然任意一个大于一的正整数都可以分解成若干质数的乘积，那么丑数也可以被分解成若干质数的乘积，且这些质数只能是 2, 3 或 5。

有了这个思路，就可以实现 isUgly 函数了：

class Solution {
public:
    /**
     * 判断一个数是否为丑数
     * @param n 要判断的数
     * @return 如果 n 是丑数返回 true，否则返回 false
     */
    bool isUgly(int n) {
        if (n <= 0) return false;
        // 如果 n 是丑数，分解因子应该只有 2, 3, 5
        while (n % 2 == 0) n /= 2;
        while (n % 3 == 0) n /= 3;
        while (n % 5 == 0) n /= 5;
        // 如果能够成功分解，说明是丑数
        return n == 1;
    }
};

丑数II

题目

给你输入一个 n，让你计算第 n 个丑数是多少，函数签名如下：

int nthUglyNumber(int n)

思路

比如输入 n = 10，函数应该返回 12，因为从小到大的丑数序列为 1, 2, 3, 4, 5, 6, 8, 9, 10, 12，第 10 个丑数是 12（注意我们把 1 也算作一个丑数）。

这道题很精妙，你看着它好像是道数学题，实际上它却是一个合并多个有序链表的问题，同时用到了筛选素数的思路。

基于筛数法的思路和丑数的定义，我们不难想到这样一个规律：如果一个数 x 是丑数，那么 x * 2, x * 3, x * 5 都一定是丑数。

如果我们把所有丑数想象成一个从小到大排序的链表，就是这个样子：

1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 8 -> ...

然后，我们可以把丑数分为三类：2 的倍数、3 的倍数、5 的倍数。这三类丑数就好像三条有序链表，如下：

能被 2 整除的丑数：

1*2 -> 2*2 -> 3*2 -> 4*2 -> 5*2 -> 6*2 -> 8*2 ->...

能被 3 整除的丑数：

1*3 -> 2*3 -> 3*3 -> 4*3 -> 5*3 -> 6*3 -> 8*3 ->...

能被 5 整除的丑数：

1*5 -> 2*5 -> 3*5 -> 4*5 -> 5*5 -> 6*5 -> 8*5 ->...

我们如果把这三条「有序链表」合并在一起并去重，得到的就是丑数的序列，其中第 n 个元素就是题目想要的答案：

1 -> 1*2 -> 1*3 -> 2*2 -> 1*5 -> 3*2 -> 4*2 ->...

class Solution {
public:
    int nthUglyNumber(int n) {
        // 可以理解为三个指向有序链表头结点的指针
        int p2 = 1, p3 = 1, p5 = 1;
        // 可以理解为三个有序链表的头节点的值
        int product2 = 1, product3 = 1, product5 = 1;
        // 可以理解为最终合并的有序链表（结果链表）
        vector<int> ugly(n + 1);
        // 可以理解为结果链表上的指针
        int p = 1;

        // 开始合并三个有序链表，找到第 n 个丑数时结束
        while (p <= n) {
            // 取三个链表的最小结点
            int min_val = min({product2, product3, product5});
            // 将最小节点接到结果链表上
            ugly[p] = min_val;
            p++;
            // 前进对应有序链表上的指针
            if (min_val == product2) {
                product2 = 2 * ugly[p2];
                p2++;
            }
            if (min_val == product3) {
                product3 = 3 * ugly[p3];
                p3++;
            }
            if (min_val == product5) {
                product5 = 5 * ugly[p5];
                p5++;
            }
        }
        // 返回第 n 个丑数
        return ugly[n];
    }
};

我们用 p2, p3, p5 分别代表三条丑数链表上的指针，用 product2, product3, product5 代表丑数链表上节点的值，用 ugly 数组记录有序链表合并之后的结果。

超级丑数

题目

给你输入一个质数列表 primes 和一个正整数 n，请你计算第 n 个「超级丑数」。所谓超级丑数是一个所有质因数都出现在 primes 中的正整数，函数签名如下：

int nthSuperUglyNumber(int n, int* primes)

思路

如果让 primes = [2, 3, 5] 就是上道题，所以这道题是上道题的进阶版。

不过思路还是类似的，你还是把每个质因子看做一条有序链表，上道题相当于让你合并三条有序链表，而这道题相当于让你合并 len(primes) 条有序链表。

我们不能用 min 函数计算最小头结点了，而是要用优先级队列来计算最小头结点，同时依然要维护链表指针、指针所指节点的值，我们可以用一个三元组来保存这些信息。

class Solution {
public:
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        // 优先队列中装三元组 int[] {product, prime, pi}
        // 其中 product 代表链表节点的值，prime 是计算下一个节点所需的质数因子，pi 代表链表上的指针
        priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;
        
        // 把多条链表的头结点加入优先级队列
        for (int i = 0; i < primes.size(); i++) {
            pq.push({1, primes[i], 1});
        }

        // 可以理解为最终合并的有序链表（结果链表）
        vector<int> ugly(n+1,0);
        // 可以理解为结果链表上的指针
        int p = 1;

        while(p <= n){
            // 取三个链表的最小结点
            auto u = pq.top();
            pq.pop();
            int product = u[0];
            int prime = u[1];
            int index = u[2];

            // 避免结果链表出现重复元素
            if (product != ugly[p - 1]) {
                // 接到结果链表上
                ugly[p] = product;
                p++;
            }

            // 生成下一个节点加入优先级队列
            pq.push({ugly[index] * prime, prime, index+1});
        }

        return ugly[n];
    }
};

丑数III

题目

给你四个整数：n, a, b, c，请你设计一个算法来找出第 n 个丑数。其中丑数是可以被 a 或 b 或 c 整除的正整数。

思路

这道题和之前题目的不同之处在于它改变了「丑数」的定义，只要一个正整数 x 存在 a, b, c 中的任何一个因子，那么 x 就是丑数。

比如输入 n = 7, a = 3, b = 4, c = 5，那么算法输出 10，因为符合条件的丑数序列为 3, 4, 5, 6, 8, 9, 10, ...，其中第 7 个数字是 10。

有了之前几道题的铺垫，你肯定可以想到把 a, b, c 的倍数抽象成三条有序链表：

1*3 -> 2*3 -> 3*3 -> 4*3 -> 5*3 -> 6*3 -> 7*3 ->...
1*4 -> 2*4 -> 3*4 -> 4*4 -> 5*4 -> 6*4 -> 7*4 ->...
1*5 -> 2*5 -> 3*5 -> 4*5 -> 5*5 -> 6*5 -> 7*5 ->...

然后将这三条链表合并成一条有序链表并去除重复元素，这样合并后的链表元素就是丑数序列，我们从中找到第 n 个元素即可：

1*3 -> 1*4 -> 1*5 -> 2*3 -> 2*4 -> 3*3 -> 2*5 ->...

有了这个思路，可以直接写出代码：

class Solution {
    public int nthUglyNumber(int n, int a, int b, int c) {
        // 可以理解为三个有序链表的头结点的值
        // 由于数据规模较大，用 long 类型
        long productA = a, productB = b, productC = c;
        // 可以理解为合并之后的有序链表上的指针
        int p = 1;

        long min = -666;

        // 开始合并三个有序链表，获取第 n 个节点的值
        while (p <= n) {
            // 取三个链表的最小结点
            min = Math.min(Math.min(productA, productB), productC);
            p++;
            // 前进最小结点对应链表的指针
            if (min == productA) {
                productA += a;
            }
            if (min == productB) {
                productB += b;
            }
            if (min == productC) {
                productC += c;
            }
        }
        return (int) min;
    }
}

这个思路应该是非常简单的，但是提交之后并不能通过所有测试用例，会超时。

注意题目给的数据范围非常大，a, b, c, n 的大小可以达到 10^9，所以即便上述算法的时间复杂度是 O(n)，也是相对比较耗时的，应该有更好的思路能够进一步降低时间复杂度。

数学 + 二分搜索

首先，我们可以定义一个单调递增的函数 f：

f(num, a, b, c) 计算 [1..num] 中，能够整除 a 或 b 或 c 的数字的个数，显然函数 f 的返回值是随着 num 的增加而增加的（单调递增）。

题目让我们求第 n 个能够整除 a 或 b 或 c 的数字是什么，也就是说我们要找到一个最小的 num，使得 f(num, a, b, c) == n。

这个 num 就是第 n 个能够整除 a 或 b 或 c 的数字。

想求参数 num 的最小值，就可以运用搜索左侧边界的二分查找算法了：

// 求第 n 个丑数
int nthUglyNumber(int n, int a, int b, int c) {
    // 题目说本题结果在 [1, 2 * 10^9] 范围内，
    // 所以就按照这个范围初始化两端都闭的搜索区间
    int left = 1, right = (int) 2e9;
    // 搜索左侧边界的二分搜索
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (f(mid, a, b, c) < n) {
            // [1..mid] 中符合条件的元素个数不足 n，所以目标在右半边
            left = mid + 1;
        } else {
            // [1..mid] 中符合条件的元素个数大于 n，所以目标在左半边
            right = mid - 1;
        }
    }
    return left;
}

// 函数 f 是一个单调函数
// 计算 [1..num] 之间有多少个能够被 a 或 b 或 c 整除的数字
long f(int num, int a, int b, int c) {
   // 见下文
}

关键说一下函数 f 怎么实现，这里面涉及集合论定理以及最小公因数、最小公倍数的计算方法。

首先，我把 [1..num] 中能够整除 a 的数字归为集合 A，能够整除 b 的数字归为集合 B，能够整除 c 的数字归为集合 C，那么 len(A) = num / a, len(B) = num / b, len(C) = num / c，这个很好理解。

但是 f(num, a, b, c) 的值肯定不是 num / a + num / b + num / c 这么简单，因为你注意有些数字可能可以被 a, b, c 中的两个数或三个数同时整除，如下图：

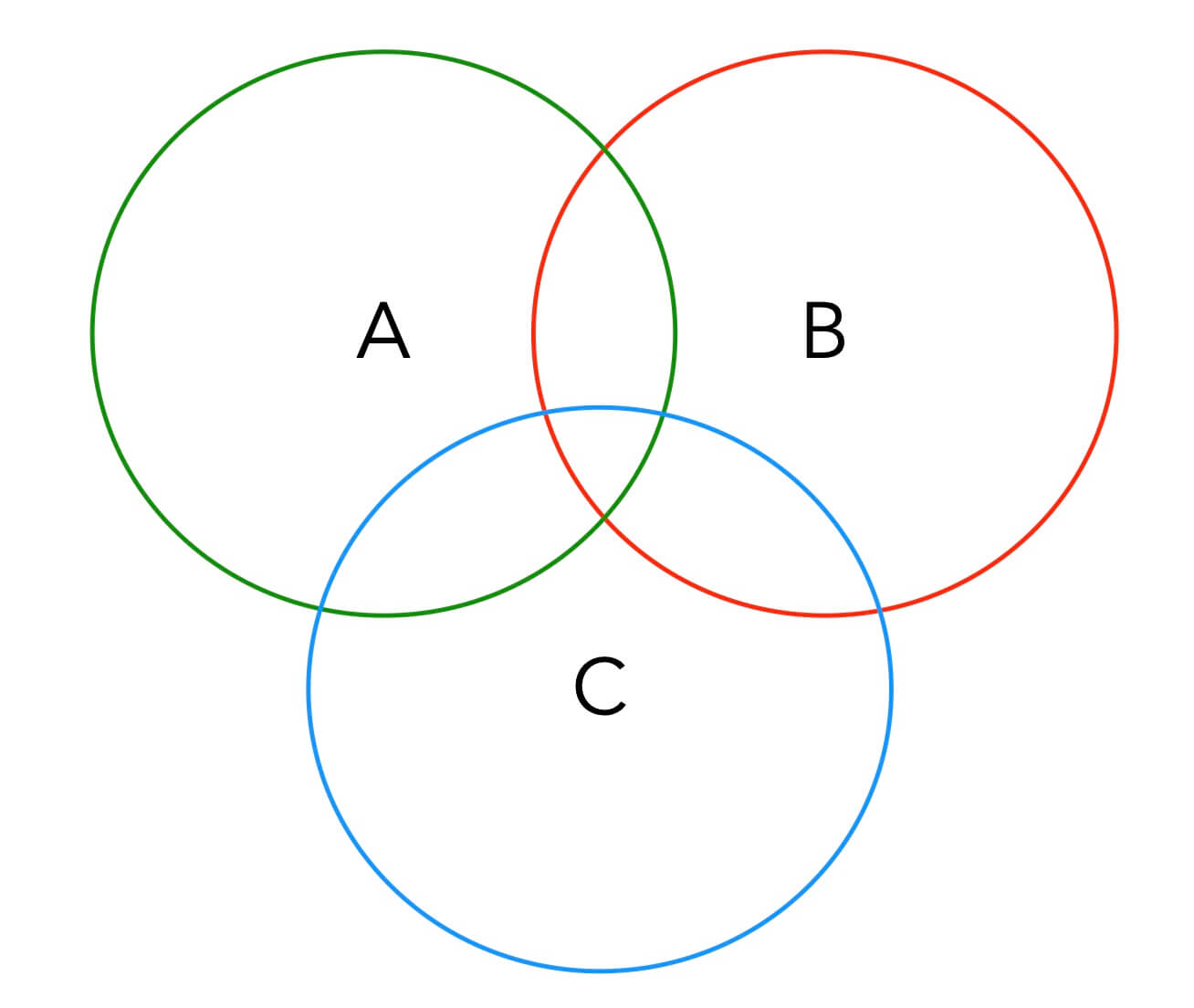
按照集合论的算法，这个集合中的元素应该是：A + B + C - A ∩ B - A ∩ C - B ∩ C + A ∩ B ∩ C。结合上图应该很好理解。

问题来了，A, B, C 三个集合的元素个数我们已经算出来了，但如何计算像 A ∩ B 这种交集的元素个数呢？

其实也很容易想明白，A ∩ B 的元素个数就是 num / lcm(a, b)，其中 lcm 是计算最小公倍数（Least Common Multiple）的函数。

类似的，A ∩ B ∩ C 的元素个数就是 num / lcm(lcm(a, b), c) 的值。

现在的问题是，最小公倍数怎么求？

直接记住定理吧：lcm(a, b) = a \* b / gcd(a, b)，其中 gcd 是计算最大公因数（Greatest Common Divisor）的函数。

现在的问题是，最大公因数怎么求？这应该是经典算法了，我们一般叫辗转相除算法（或者欧几里得算法）。

好了，套娃终于套完了，我们可以把上述思路翻译成代码就可以实现 f 函数，注意本题数据规模比较大，有时候需要用 long 类型防止 int 溢出：

// 计算最大公因数（辗转相除/欧几里得算法）
long gcd(long a, long b) {
    if (a < b) {
        // 保证 a > b
        return gcd(b, a);
    }
    if (b == 0) {
        return a;
    }
    return gcd(b, a % b);
}

// 最小公倍数
long lcm(long a, long b) {
    // 最小公倍数就是乘积除以最大公因数
    return a * b / gcd(a, b);
}

// 计算 [1..num] 之间有多少个能够被 a 或 b 或 c 整除的数字
long f(int num, int a, int b, int c) {
    long setA = num / a, setB = num / b, setC = num / c;
    long setAB = num / lcm(a, b);
    long setAC = num / lcm(a, c);
    long setBC = num / lcm(b, c);
    long setABC = num / lcm(lcm(a, b), c);
    // 集合论定理：A + B + C - A ∩ B - A ∩ C - B ∩ C + A ∩ B ∩ C
    return setA + setB + setC - setAB - setAC - setBC + setABC;
}

分治算法 详解：运算优先级

实际上，很多算法问题不具备动态规划问题的重叠子问题、最优子结构等特性，但都可以用「分解问题」的思路来解决，我们可以给这些算法一个高大上的名字，统称为「分治算法」。

添加括号的所有方式

题目

给你一个由数字和运算符组成的字符串 expression ，按不同优先级组合数字和运算符，计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。

生成的测试用例满足其对应输出值符合 32 位整数范围，不同结果的数量不超过 104 。

示例 1：

输入：expression = "2-1-1"
输出：[0,2]
解释：
((2-1)-1) = 0 
(2-(1-1)) = 2

示例 2：

输入：expression = "2*3-4*5"
输出：[-34,-14,-10,-10,10]
解释：
(2*(3-(4*5))) = -34 
((2*3)-(4*5)) = -14 
((2*(3-4))*5) = -10 
(2*((3-4)*5)) = -10 
(((2*3)-4)*5) = 10

提示：

• 1 <= expression.length <= 20
• expression 由数字和算符 '+'、'-' 和 '*' 组成。
• 输入表达式中的所有整数值在范围 [0, 99]

// 计算所有加括号的结果
std::vector<int> diffWaysToCompute(std::string input);

思路

看到这道题的第一感觉肯定是复杂，我要穷举出所有可能的加括号方式，是不是还要考虑括号的合法性？是不是还要考虑计算的优先级？

是的，这些都要考虑，但是不需要我们来考虑。利用分治思想和递归函数，算法会帮我们考虑一切细节。

解决本题的关键有两点：

1、不要思考整体，而是把目光聚焦局部，只看一个运算符。

说白了，解决递归相关的算法问题，就是一个化整为零的过程，你必须瞄准一个小的突破口，然后把问题拆解，大而化小，利用递归函数来解决。

2、明确递归函数的定义是什么，相信并且利用好函数的定义。

这也是前文经常提到的一个点，因为递归函数要自己调用自己，你必须搞清楚函数到底能干嘛，才能正确进行递归调用。

下面来具体解释下这两个关键点怎么理解。

我们先举个例子，比如我给你输入这样一个算式：

1 + 2 * 3 - 4 * 5

请问，这个算式有几种加括号的方式？请在一秒之内回答我。

估计你回答不出来，因为括号可以嵌套，要穷举出来肯定得费点功夫。

不过呢，嵌套这个事情吧，我们人类来看是很头疼的，但对于算法来说嵌套括号不要太简单，一次递归就可以嵌套一层，一次搞不定大不了多递归几次。

所以，作为写算法的人类，我们只需要思考，如果不让括号嵌套（即只加一层括号），有几种加括号的方式？

还是上面的例子，显然我们有四种加括号方式：

(1) + (2 * 3 - 4 * 5)
(1 + 2) * (3 - 4 * 5)
(1 + 2 * 3) - (4 * 5)
(1 + 2 * 3 - 4) * (5)

发现规律了么？其实就是按照运算符进行分割，给每个运算符的左右两部分加括号，这就是之前说的第一个关键点，不要考虑整体，而是聚焦每个运算符。

现在单独说上面的第三种情况：

(1 + 2 * 3) - (4 * 5)

我们用减号 - 作为分隔，把原算式分解成两个算式 1 + 2 * 3 和 4 * 5。

分治分治，分而治之，这一步就是把原问题进行了「分」，我们现在要开始「治」了。

1 + 2 * 3 可以有两种加括号的方式，分别是：

(1) + (2 * 3) = 7
(1 + 2) * (3) = 9

或者我们可以写成这种形式：

1 + 2 * 3 = [9, 7]

而 4 * 5 当然只有一种加括号方式，就是 4 * 5 = [20]。

然后呢，你能不能通过上述结果推导出 (1 + 2 * 3) - (4 * 5) 有几种加括号方式，或者说有几种不同的结果？

显然，可以推导出来 (1 + 2 * 3) - (4 * 5) 有两种结果，分别是：

9 - 20 = -11
7 - 20 = -13

那你可能要问了， 1 + 2 * 3 = [9, 7] 的结果是我们自己看出来的，如何让算法计算出来这个结果呢？

这个简单啊，再回头看下题目给出的函数签名：

// 定义：计算算式 input 所有可能的运算结果
vector<int> diffWaysToCompute(string input);

这个函数不就是干这个事儿的吗？这就是我们之前说的第二个关键点，明确函数的定义，相信并且利用这个函数定义。

你甭管这个函数怎么做到的，你相信它能做到，然后用就行了，最后它就真的能做到了。

那么，对于 (1 + 2 * 3) - (4 * 5) 这个例子，我们的计算逻辑其实就是这段代码：

vector<int> diffWaysToCompute(string input) {
    vector<int> res;
    // ****** 分 ******
    vector<int> left = diffWaysToCompute("1 + 2 * 3");
    vector<int> right = diffWaysToCompute("4 * 5");
    // ****** 治 ******
    for (int a : left)
        for (int b : right)
            res.push_back(a - b);

    return res;
}

好，现在 (1 + 2 * 3) - (4 * 5) 这个例子是如何计算的，你应该完全理解了吧，那么回来看我们的原始问题。

原问题 1 + 2 * 3 - 4 * 5 是不是只有 (1 + 2 * 3) - (4 * 5) 这一种情况？是不是只能从减号 - 进行分割？

不是，每个运算符都可以把原问题分割成两个子问题，刚才已经列出了所有可能的分割方式：

(1) + (2 * 3 - 4 * 5)
(1 + 2) * (3 - 4 * 5)
(1 + 2 * 3) - (4 * 5)
(1 + 2 * 3 - 4) * (5)

所以，我们需要穷举上述的每一种情况，可以进一步细化一下解法代码：

class Solution {
public:
    vector<int> diffWaysToCompute(string input) {
        vector<int> res; 
        for (int i = 0; i < input.size(); i++) {
            char c = input[i];
            // 扫描算式 input 中的运算符
            if (c == '-' || c == '*' || c == '+') {
                // ****** 分 ******
                // 以运算符为中心，分割成两个字符串，分别递归计算
                vector<int> left = diffWaysToCompute(input.substr(0, i)); 
                vector<int> right = diffWaysToCompute(input.substr(i + 1));
                // ****** 治 ******
                // 通过子问题的结果，合成原问题的结果
                for (int a : left)
                    for (int b : right)
                        if (c == '+')
                            res.push_back(a + b);
                        else if (c == '-')
                            res.push_back(a - b);
                        else if (c == '*')
                            res.push_back(a * b);
            }
        }
        // base case
        // 如果 res 为空，说明算式是一个数字，没有运算符
        if (res.empty()) {
            res.push_back(stoi(input));
        }
        return res;
    }
};

有了刚才的铺垫，这段代码应该很好理解了吧，就是扫描输入的算式 input，每当遇到运算符就进行分割，递归计算出结果后，根据运算符来合并结果。

这就是典型的分治思路，先「分」后「治」，先按照运算符将原问题拆解成多个子问题，然后通过子问题的结果来合成原问题的结果。

当然，一个重点在这段代码：

// base case
// 如果res为空，说明算式是一个数字，没有运算符
if (res.empty()) {
    res.push_back(stoi(input));
}

递归函数必须有个 base case 用来结束递归，其实这段代码就是我们分治算法的 base case，代表着你「分」到什么时候可以开始「治」。

我们是按照运算符进行「分」的，一直这么分下去，什么时候是个头？显然，当算式中不存在运算符的时候就可以结束了。

那为什么以 res.isEmpty() 作为判断条件？因为当算式中不存在运算符的时候，就不会触发 if 语句，也就不会给 res 中添加任何元素。

至此，这道题的解法代码就写出来了，但是时间复杂度是多少呢？

如果单看代码，真的很难通过 for 循环的次数看出复杂度是多少，所以我们需要改变思路，本题在求所有可能的计算结果，不就相当于在求算式 input 的所有合法括号组合吗？

那么，对于一个算式，有多少种合法的括号组合呢？这就是著名的「卡特兰数」了，最终结果是一个组合数。

剪枝优化

其实本题还有一个小的优化，可以进行递归剪枝，减少一些重复计算，比如说输入的算式如下：

1 + 1 + 1 + 1 + 1

那么按照算法逻辑，按照运算符进行分割，一定存在下面两种分割情况：

(1 + 1) + (1 + 1 + 1)
(1 + 1 + 1) + (1 + 1)

算法会依次递归每一种情况，其实就是冗余计算嘛，所以我们可以对解法代码稍作修改，加一个备忘录来避免这种重复计算：

class Solution {
public:
    // 备忘录
    unordered_map<string, vector<int>> memo;

    vector<int> diffWaysToCompute(string input) {
        // 避免重复计算
        if (memo.count(input)) {
            return memo[input];
        }
        // ****** 其他都不变 ******
        vector<int> res;
        for (int i = 0; i < input.length(); i++) {
            // ...
        }
        if (res.empty()) {
            res.push_back(stoi(input));
        }
        // ***********************

        // 将结果添加进备忘录
        memo[input] = res;
        return res;
    }
};

斗地主算法

斗地主中，大小连续的牌可以作为顺子，有时候我们把对子拆掉，结合单牌，可以组合出更多的顺子，可能更容易赢。

那么如何合理拆分手上的牌，合理地拆出顺子呢？

题目

给你输入一个升序排列的数组 nums（可能包含重复数字），请你判断 nums 是否能够被分割成若干个长度至少为 3 的子序列，每个子序列都由连续的整数组成。

函数签名如下：

bool isPossible(vector<int>& nums);

思路

比如题目举的例子，输入 nums = [1,2,3,3,4,4,5,5]，算法返回 true。

因为 nums 可以被分割成 [1,2,3,4,5] 和 [3,4,5] 两个包含连续整数子序列。

但如果输入 nums = [1,2,3,4,4,5]，算法返回 false，因为无法分割成两个长度至少为 3 的连续子序列。

对于这种涉及连续整数的问题，应该条件反射地想到排序，不过题目说了，输入的 nums 本就是排好序的。

那么，我们如何判断 nums 是否能够被划分成若干符合条件的子序列呢？

我们想把 nums 的元素划分到若干个子序列中，其实就是下面这个代码逻辑：

for (int v : nums) {
    if (...) {
        // 将 v 分配到某个子序列中
    } else {
        // 实在无法分配 v
        return false;
    }
    return true;
}

关键在于，我们怎么知道当前元素 v 如何进行分配呢？

肯定得分情况讨论，把情况讨论清楚了，题目也就做出来了。

总共有两种情况：

1、当前元素 v 自成一派，「以自己开头」构成一个长度至少为 3 的序列。

比如输入 nums = [1,2,3,6,7,8]，遍历到元素 6 时，它只能自己开头形成一个符合条件的子序列 [6,7,8]。

2、当前元素 v 接到已经存在的子序列后面。

比如输入 nums = [1,2,3,4,5]，遍历到元素 4 时，它只能接到已经存在的子序列 [1,2,3] 后面。它没办法自成开头形成新的子序列，因为少了个 6。

但是，如果这两种情况都可以，应该如何选择？

比如说，输入 nums = [1,2,3,4,5,5,6,7]，对于元素 4，你说它应该形成一个新的子序列 [4,5,6] 还是接到子序列 [1,2,3] 后面呢？

显然，nums 数组的正确划分方法是分成 [1,2,3,4,5] 和 [5,6,7]，所以元素 4 应该优先判断自己是否能够接到其他序列后面，如果不行，再判断是否可以作为新的子序列开头。

这就是整体的思路，想让算法代码实现这两个选择，需要两个哈希表来做辅助：

freq 哈希表帮助一个元素判断自己是否能够作为开头，need 哈希表帮助一个元素判断自己是否可以被接到其他序列后面。

freq 记录每个元素出现的次数，比如 freq[3] == 2 说明元素 3 在 nums 中出现了 2 次。

那么如果我发现 freq[3], freq[4], freq[5] 都是大于 0 的，那就说明元素 3 可以作为开头组成一个长度为 3 的子序列。

need 记录哪些元素可以被接到其他子序列后面。

比如说现在已经组成了两个子序列 [1,2,3,4] 和 [2,3,4]，那么 need[5] 的值就应该是 2，说明对元素 5 的需求为 2。

明白了这两个哈希表的作用，我们就可以看懂解法了：

class Solution {
public:
    bool isPossible(vector<int>& nums) {
        unordered_map<int, int> freq;
        unordered_map<int, int> need;

        // 统计 nums 中元素的频率
        for (int v : nums) {
            ++freq[v];
        }

        for (int v : nums) {
            if (freq[v] == 0) {
                // 已经被用到其他子序列中
                continue;
            }

            // 先判断 v 是否能接到其他子序列后面
            if (need.count(v) && need[v] > 0) {
                // v 可以接到之前的某个序列后面
                freq[v] = freq[v] - 1;
                // 对 v 的需求减一
                need[v] = need[v] - 1;
                // 对 v + 1 的需求加一
                need[v + 1] = need[v + 1] + 1;
            } else if (freq[v] > 0 && 
                       freq[v + 1] > 0 && 
                       freq[v + 2] > 0) {
                // 将 v 作为开头，新建一个长度为 3 的子序列 [v, v+1, v+2]
                freq[v] = freq[v] - 1;
                freq[v + 1] = freq[v + 1] - 1;
                freq[v + 2] = freq[v + 2] - 1;
                // 对 v + 3 的需求加一
                need[v + 3] = need[v + 3] + 1;
            } else {
                // 两种情况都不符合，则无法分配
                return false;
            }
        }

        return true;
    }
}

至此，这道题就解决了。

那你可能会说，斗地主里面顺子至少要 5 张连续的牌，我们这道题只计算长度最小为 3 的子序列，怎么办？

很简单，把我们的 else if 分支修改一下，连续判断 v 之后的连续 5 个元素就行了。

那么，我们再难为难为自己，如果我想要的不只是一个布尔值，我想要你给我把子序列都打印出来，怎么办？

其实这也很好实现，只要修改 need，不仅记录对某个元素的需求个数，而且记录具体是哪些子序列产生的需求：

// need[6] = 2 说明有两个子序列需要 6
unordered_map<int, int> need;

// need[6] = {
//     {3,4,5},
//     {2,3,4,5},
// }
// 记录哪两个子序列需要 6
unordered_map<int, vector<vector<int>>> need;

这样，我们稍微修改一下之前的代码就行了：

class Solution {
public:
    bool isPossible(vector<int>& nums) {
        unordered_map<int, int> freq;
        unordered_map<int, vector<vector<int>>> need;

        // 统计 nums 中元素的频率
        for (int v : nums) {
            freq[v] = freq[v] + 1;
        }

        for (int v : nums) {
            if (freq[v] == 0) {
                continue;
            }

            if (need.count(v) && need[v].size() > 0) {
                // v 可以接到之前的某个序列后面
                freq[v] = freq[v] - 1;
                // 随便取一个需要 v 的子序列
                vector<int> seq = need[v].back();
                need[v].pop_back();
                // 把 v 接到这个子序列后面
                seq.push_back(v);
                // 这个子序列的需求变成了 v + 1
                need[v + 1].push_back(seq);
            } else if (freq.count(v) > 0 && 
                       freq.count(v + 1) > 0 && 
                       freq.count(v + 2) > 0) {
                // 可以将 v 作为开头
                freq[v] = freq[v] - 1;
                freq[v + 1] = freq[v + 1] - 1;
                freq[v + 2] = freq[v + 2] - 1;
                // 新建一个长度为 3 的子序列 [v,v + 1,v + 2]
                vector<int> seq = {v, v + 1, v + 2};
                // 对 v + 3 的需求加一
                need[v + 3].push_back(seq);
            } else {
                return false;
            }
        }

        // 打印切分出的所有子序列
        for (auto& entry : need) {
            for (vector<int>& seq : entry.second) {
                for (int val : seq) {
                    cout << val << " ";
                }
                cout << endl;
            }
        }

        return true;
    }
};

烧饼排序算法

假设盘子上有 n 块面积大小不一的烧饼，你如何用一把锅铲进行若干次翻转，让这些烧饼的大小有序（小的在上，大的在下）？

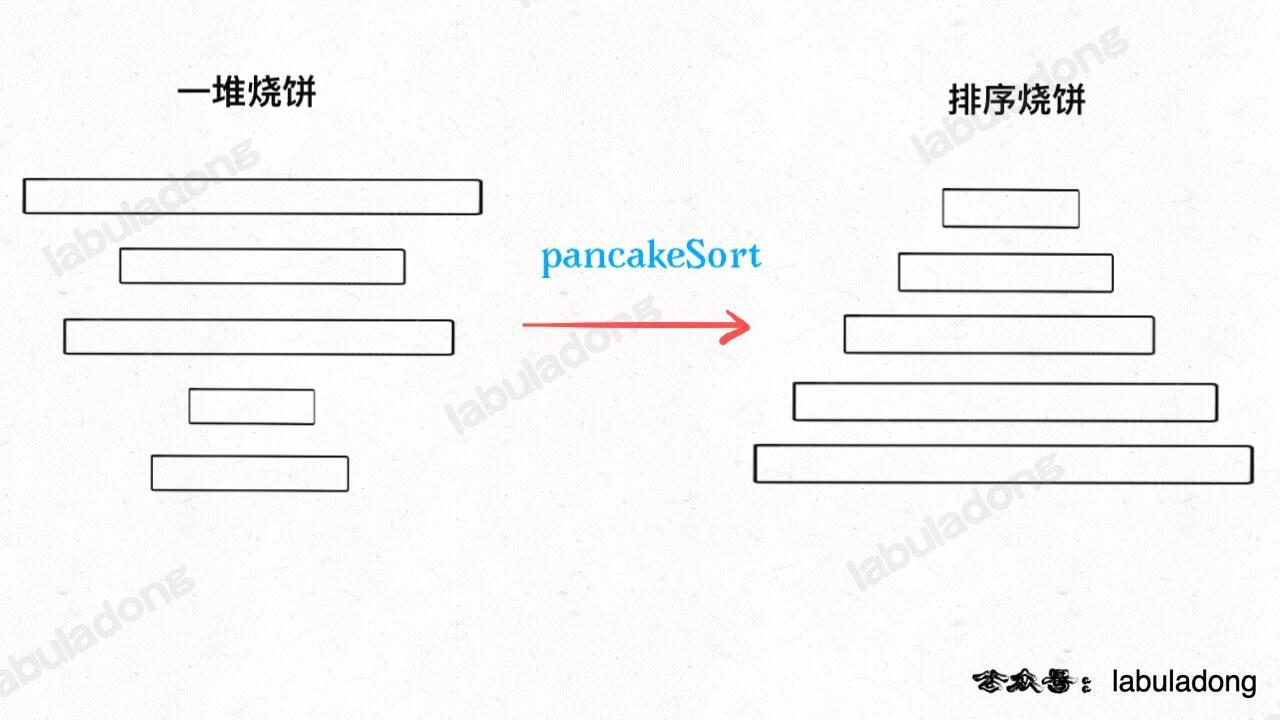
设想一下用锅铲翻转一堆烧饼的情景，其实是有一点限制的，我们每次只能将最上面的若干块饼子翻转：

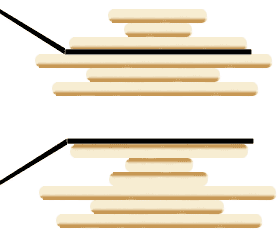
我们的问题是，如何使用算法得到一个翻转序列，使得烧饼堆变得有序？

首先，需要把这个问题抽象，用数组来表示烧饼堆：

题目

给你一个整数数组 arr ，请使用 煎饼翻转 完成对数组的排序。

一次煎饼翻转的执行过程如下：

• 选择一个整数 k ，1 <= k <= arr.length
• 反转子数组 arr[0...k-1]（下标从 0 开始）

例如，arr = [3,2,1,4] ，选择 k = 3 进行一次煎饼翻转，反转子数组 [3,2,1] ，得到 arr = [**1**,**2**,**3**,4] 。

以数组形式返回能使 arr 有序的煎饼翻转操作所对应的 k 值序列。任何将数组排序且翻转次数在 10 * arr.length 范围内的有效答案都将被判断为正确。

示例 1：

输入：[3,2,4,1]
输出：[4,2,4,3]
解释：
我们执行 4 次煎饼翻转，k 值分别为 4，2，4，和 3。
初始状态 arr = [3, 2, 4, 1]
第一次翻转后（k = 4）：arr = [1, 4, 2, 3]
第二次翻转后（k = 2）：arr = [4, 1, 2, 3]
第三次翻转后（k = 4）：arr = [3, 2, 1, 4]
第四次翻转后（k = 3）：arr = [1, 2, 3, 4]，此时已完成排序。 

示例 2：

输入：[1,2,3]
输出：[]
解释：
输入已经排序，因此不需要翻转任何内容。
请注意，其他可能的答案，如 [3，3] ，也将被判断为正确。

提示：

• 1 <= arr.length <= 100
• 1 <= arr[i] <= arr.length
• arr 中的所有整数互不相同（即，arr 是从 1 到 arr.length 整数的一个排列）

思路分析

我们需要实现这样一个函数：

// cakes 是一堆烧饼，函数会将前 n 个烧饼排序
void sort(int cakes[], int n);

如果我们找到了前 n 个烧饼中最大的那个，然后设法将这个饼子翻转到最底下：

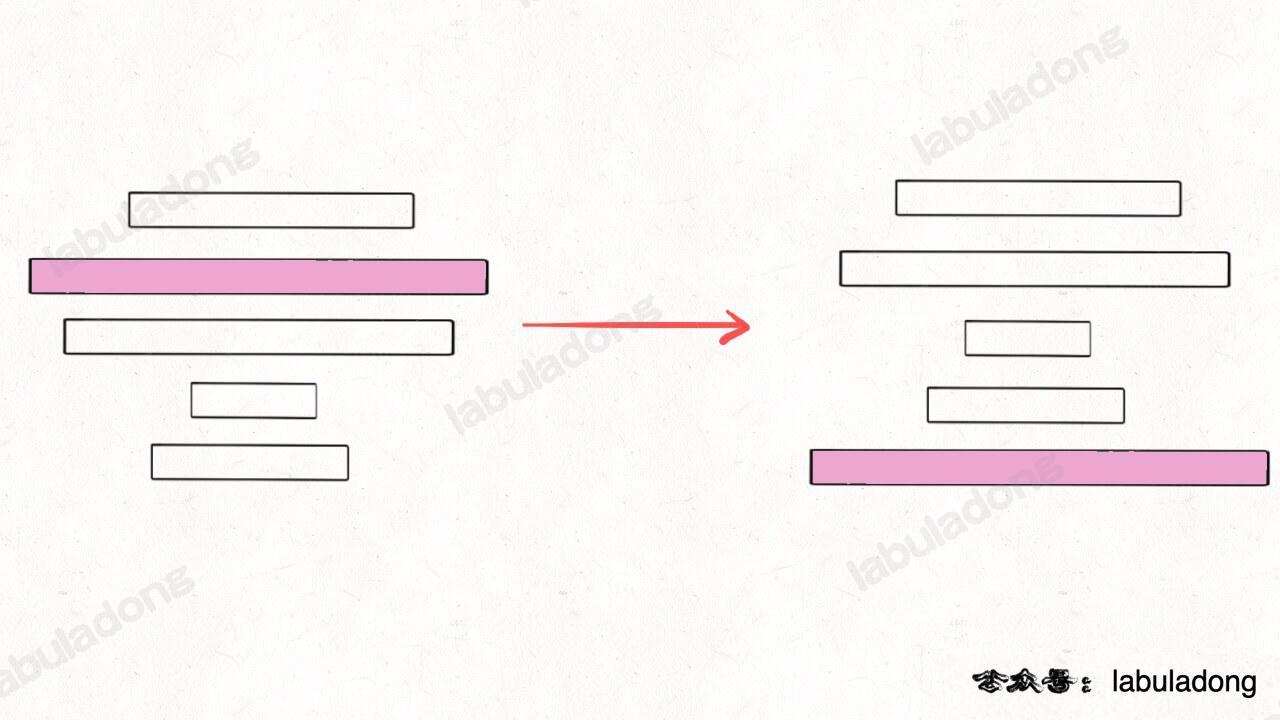
那么，原问题的规模就可以减小，递归调用 pancakeSort(A, n-1) 即可：

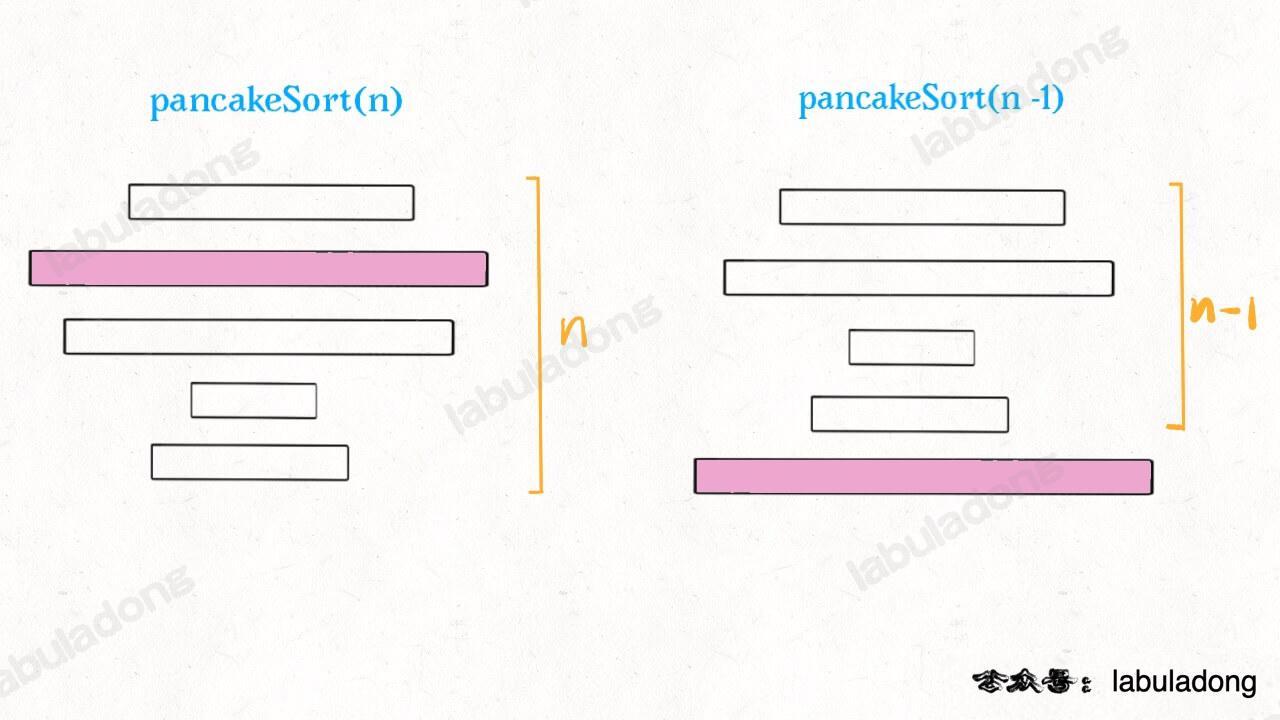
接下来，对于上面的这 n - 1 块饼，如何排序呢？还是先从中找到最大的一块饼，然后把这块饼放到底下，再递归调用 pancakeSort(A, n-1-1)……

你看，这就是递归性质，总结一下思路就是：

1、找到 n 个饼中最大的那个。

2、把这个最大的饼移到最底下。

3、递归调用 pancakeSort(A, n - 1)。

base case：n == 1 时，排序 1 个饼时不需要翻转。

那么，最后剩下个问题，如何设法将某块烧饼翻到最后呢？

其实很简单，比如第 3 块饼是最大的，我们想把它换到最后，也就是换到第 n 块。可以这样操作：

1、用锅铲将前 3 块饼翻转一下，这样最大的饼就翻到了最上面。

2、用锅铲将前 n 块饼全部翻转，这样最大的饼就翻到了第 n 块，也就是最后一块。

以上两个流程理解之后，基本就可以写出解法了，不过题目要求我们写出具体的反转操作序列，这也很简单，只要在每次翻转烧饼时记录下来就行了。

代码实现

class Solution {
public:
    // 记录反转操作序列
    vector<int> res;

    vector<int> pancakeSort(vector<int>& cakes) {
        sort(cakes, cakes.size());
        return res;
    }

    void sort(vector<int>& cakes, int n) {
        // base case
        if (n == 1) return;

        // 寻找最大饼的索引
        int maxCake = 0;
        int maxCakeIndex = 0;
        for (int i = 0; i < n; i++)
            if (cakes[i] > maxCake) {
                maxCakeIndex = i;
                maxCake = cakes[i];
            }

        // 第一次翻转，将最大饼翻到最上面
        reverse(cakes, 0, maxCakeIndex);
        res.push_back(maxCakeIndex + 1);
        // 第二次翻转，将最大饼翻到最下面
        reverse(cakes, 0, n - 1);
        res.push_back(n);

        // 递归调用
        sort(cakes, n - 1);
    }

    void reverse(vector<int>& arr, int i, int j) {
        while (i < j) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++; j--;
        }
    }
};

算法的时间复杂度很容易计算，因为递归调用的次数是 n，每次递归调用都需要一次 for 循环，时间复杂度是 O(n)，所以总的复杂度是 O(n^2)。

最后，我们可以思考一个问题：按照我们这个思路，得出的操作序列长度应该为 2(n - 1)，因为每次递归都要进行 2 次翻转并记录操作，总共有 n 层递归，但由于 base case 直接返回结果，不进行翻转，所以最终的操作序列长度应该是固定的 2(n - 1)。

字符串乘法计算

对于比较小的数字，做运算可以直接使用编程语言提供的运算符，但是如果相乘的两个因数非常大，语言提供的数据类型可能就会溢出。一种替代方案就是，运算数以字符串的形式输入，然后模仿我们小学学习的乘法算术过程计算出结果，并且也用字符串表示。

题目

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

注意：不能使用任何内置的 BigInteger 库或直接将输入转换为整数。

示例 1:

输入: num1 = "2", num2 = "3"
输出: "6"

示例 2:

输入: num1 = "123", num2 = "456"
输出: "56088"

提示：

• 1 <= num1.length, num2.length <= 200
• num1 和 num2 只能由数字组成。
• num1 和 num2 都不包含任何前导零，除了数字0本身。

思路

唯一的思路就是模仿我们手算乘法。

比如说我们手算 123 × 45，应该会这样计算：

计算 123 × 5，再计算 123 × 4，最后错一位相加。这个流程恐怕小学生都可以熟练完成，但是你是否能把这个运算过程进一步机械化，写成一套算法指令让没有任何智商的计算机来执行呢？

你看这个简单过程，其中涉及乘法进位，涉及错位相加，还涉及加法进位；而且还有一些不易察觉的问题，比如说两位数乘以两位数，结果可能是四位数，也可能是三位数，你怎么想出一个标准化的处理方式？这就是算法的魅力，如果没有计算机思维，简单的问题可能都没办法自动化处理。

首先，我们这种手算方式还是太「高级」了，我们要再「低级」一点，123 × 5 和 123 × 4 的过程还可以进一步分解，最后再相加：

现在 123 并不大，如果是个很大的数字的话，是无法直接计算乘积的。我们可以用一个数组在底下接收相加结果：

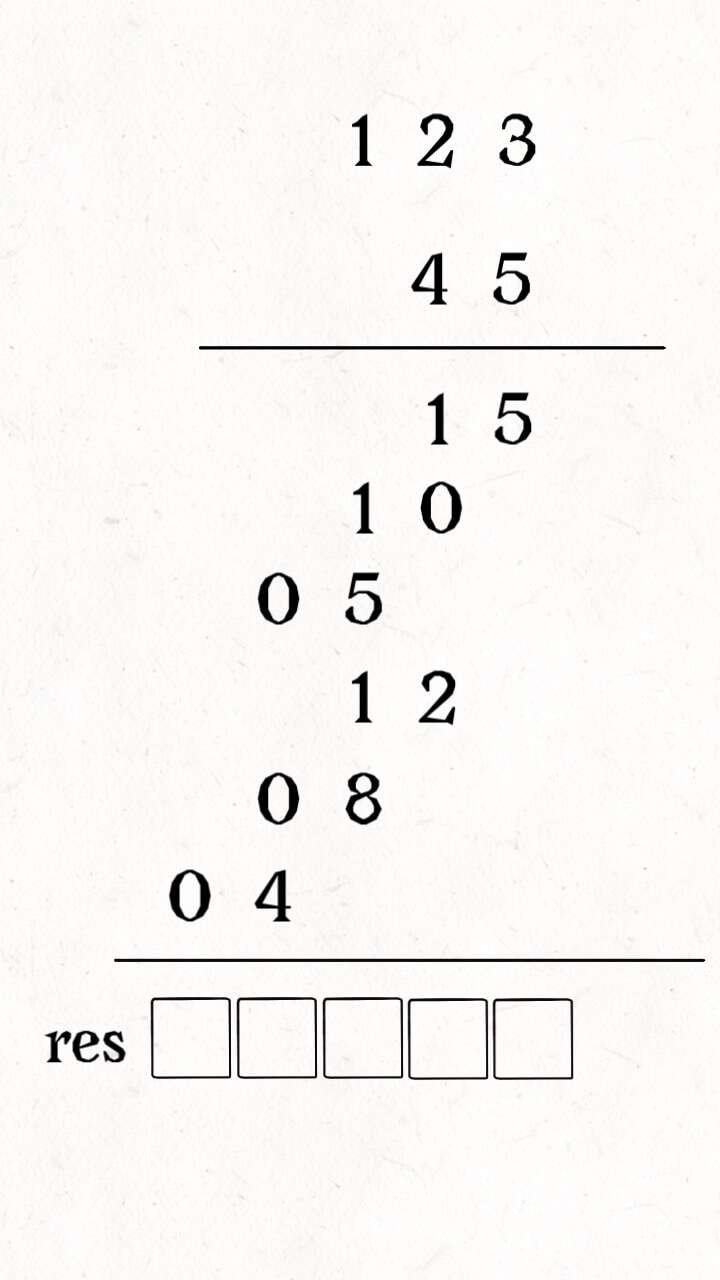
整个计算过程大概是这样，有两个指针 i，j 在 num1 和 num2 上游走，计算乘积，同时将乘积叠加到 res 的正确位置，如下 GIF 图所示：

现在还有一个关键问题，如何将乘积叠加到 res 的正确位置，或者说，如何通过 i，j 计算 res 的对应索引呢？

其实，细心观察之后就发现，num1[i] 和 num2[j] 的乘积对应的就是 res[i+j] 和 res[i+j+1] 这两个位置。

明白了这一点，就可以用代码模仿出这个计算过程了：

class Solution {
public:
    string multiply(string num1, string num2) {
        int m = num1.size(), n = num2.size();
        // 结果最多为 m + n 位数
        vector<int> res(m + n);
        // 从个位数开始逐位相乘
        for (int i = m - 1; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                int mul = (num1[i] - '0') * (num2[j] - '0');
                // 乘积在 res 对应的索引位置
                int p1 = i + j, p2 = i + j + 1;
                // 叠加到 res 上
                int sum = mul + res[p2];
                res[p2] = sum % 10;
                res[p1] += sum / 10;
            }
        }
        // 结果前缀可能存的 0（未使用的位）
        int i = 0;
        while (i < res.size() && res[i] == 0)
            i++;
        // 将计算结果转化成字符串
        string str;
        for (; i < res.size(); i++)
            str.push_back(res[i]+'0');
        
        return str.empty() ? "0" : str;
    }
};

至此，字符串乘法算法就完成了。

总结一下，我们习以为常的一些思维方式，在计算机看来是非常难以做到的。比如说我们习惯的算术流程并不复杂，但是如果让你再进一步，翻译成代码逻辑，并不简单。算法需要将计算流程再简化，通过边算边叠加的方式来得到结果。

俗话教育我们，不要陷入思维定式，不要程序化，要发散思维，要创新。但我觉得程序化并不是坏事，可以大幅提高效率，减小失误率。算法不就是一套程序化的思维吗，只有程序化才能让计算机帮助我们解决复杂问题呀！

也许算法就是一种寻找思维定式的思维吧。

高效接雨水

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

核心思路

所以对于这种问题，我们不要想整体，而应该去想局部；就像之前的文章写的动态规划问题处理字符串问题，不要考虑如何处理整个字符串，而是去思考应该如何处理每一个字符。

这么一想，可以发现这道题的思路其实很简单。具体来说，仅仅对于位置 i，能装下多少水呢？

能装 2 格水，因为 height[i] 的高度为 0，而这里最多能盛 2 格水，2-0=2。

为什么位置 i 最多能盛 2 格水呢？因为，位置 i 能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关，我们分别称这两个柱子高度为 l_max 和 r_max；位置 i 最大的水柱高度就是 min(l_max, r_max)。

更进一步，对于位置 i，能够装的水为：

water[i] = min(
    # 左边最高的柱子
    max(height[0..i]),  
    # 右边最高的柱子
    max(height[i..end]) 
) - height[i]

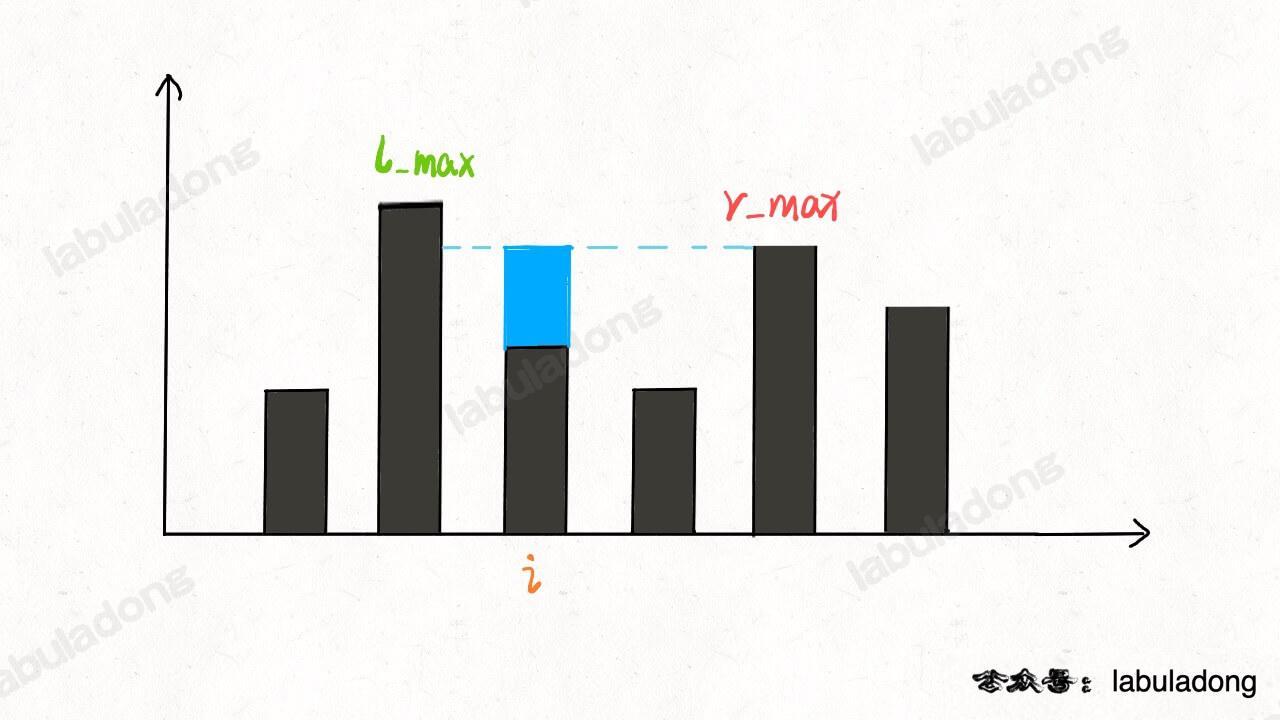
这就是本问题的核心思路，我们可以简单写一个暴力算法：

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        int res = 0;
        for (int i = 1; i < n - 1; i++) {
            int l_max = 0, r_max = 0;
            // 找右边最高的柱子
            for (int j = i; j < n; j++)
                r_max = max(r_max, height[j]);
            // 找左边最高的柱子
            for (int j = i; j >= 0; j--)
                l_max = max(l_max, height[j]);
            // 如果自己就是最高的话，
            // l_max == r_max == height[i]
            res += min(l_max, r_max) - height[i];
        }
        return res;
    }
};

有之前的思路，这个解法应该是很直接粗暴的，时间复杂度 O(N^2)，空间复杂度 O(1)。但是很明显这种计算 r_max 和 l_max 的方式非常笨拙，一般的优化方法就是备忘录。

备忘录优化

之前的暴力解法，不是在每个位置 i 都要计算 r_max 和 l_max 吗？我们直接把结果都提前计算出来，别傻不拉几的每次都遍历，这时间复杂度不就降下来了嘛。

我们开两个数组 r_max 和 l_max 充当备忘录，l_max[i] 表示位置 i 左边最高的柱子高度，r_max[i] 表示位置 i 右边最高的柱子高度。预先把这两个数组计算好，避免重复计算：

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.empty()) {
            return 0;
        }
        int n = height.size();
        int res = 0;
        //Array acts as a memo
        vector<int> l_max(n);
        vector<int> r_max(n);
        //Initialize base case
        l_max[0] = height[0];
        r_max[n - 1] = height[n - 1];
        //Calculate l_max from left to right
        for (int i = 1; i < n; i++)
            l_max[i] = max(height[i], l_max[i - 1]);
        //Calculate r_max from right to left
        for (int i = n - 2; i >= 0; i--)
            r_max[i] = max(height[i], r_max[i + 1]);
        //Calculate the answer
        for (int i = 1; i < n - 1; i++)
            res += min(l_max[i], r_max[i]) - height[i];


        return res;
    }
};

这个优化其实和暴力解法思路差不多，就是避免了重复计算，把时间复杂度降低为 O(N)，已经是最优了，但是空间复杂度是 O(N)。下面来看一个精妙一些的解法，能够把空间复杂度降低到 O(1)。

双指针解法

这种解法的思路是完全相同的，但在实现手法上非常巧妙，我们这次也不要用备忘录提前计算了，而是用双指针边走边算，节省下空间复杂度。

首先，看一部分代码：

int trap(vector<int>& height) {
    int left = 0, right = height.size() - 1;
    int l_max = 0, r_max = 0;

    while (left < right) {
        l_max = max(l_max, height[left]); // 从左端开始求左侧柱子高度的最大值
        r_max = max(r_max, height[right]); // 从右端开始求右侧柱子高度的最大值
        // 在此处 l_max 和 r_max 分别表示左右两侧柱子当前可盛雨水的最大高度
        left++; right--;
    }
}

对于这部分代码，请问 l_max 和 r_max 分别表示什么意义呢？

很容易理解，l_max 是 height[0..left] 中最高柱子的高度，r_max 是 height[right..end] 的最高柱子的高度。

明白了这一点，直接看解法：

class Solution {
public:
    int trap(vector<int>& height) {
        int left = 0, right = height.size() - 1;
        int l_max = 0, r_max = 0;

        int res = 0;
        while (left < right) {
            l_max = max(l_max, height[left]);
            r_max = max(r_max, height[right]);

            // res += min(l_max, r_max) - height[i]
            if (l_max < r_max) {
                res += l_max - height[left];
                left++;
            } else {
                res += r_max - height[right];
                right--;
            }
        }
        return res;
    }
};

你看，其中的核心思想和之前一模一样，换汤不换药。但是细心的读者可能会发现次解法还是有点细节差异：

之前的备忘录解法，l_max[i] 和 r_max[i] 分别代表 height[0..i] 和 height[i..end] 的最高柱子高度。

res += Math.min(l_max[i], r_max[i]) - height[i];

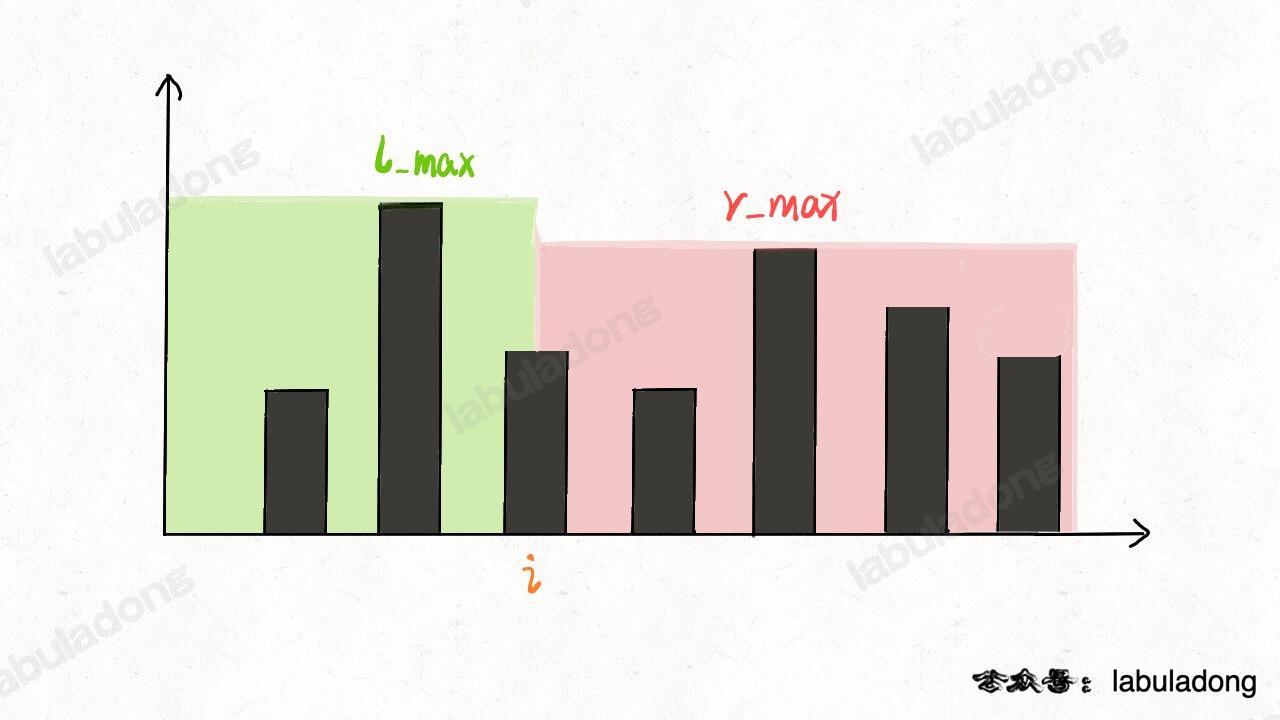
但是双指针解法中，l_max 和 r_max 代表的是 height[0..left] 和 height[right..end] 的最高柱子高度。比如这段代码：

if (l_max < r_max) {
    res += l_max - height[left];
    left++; 
}

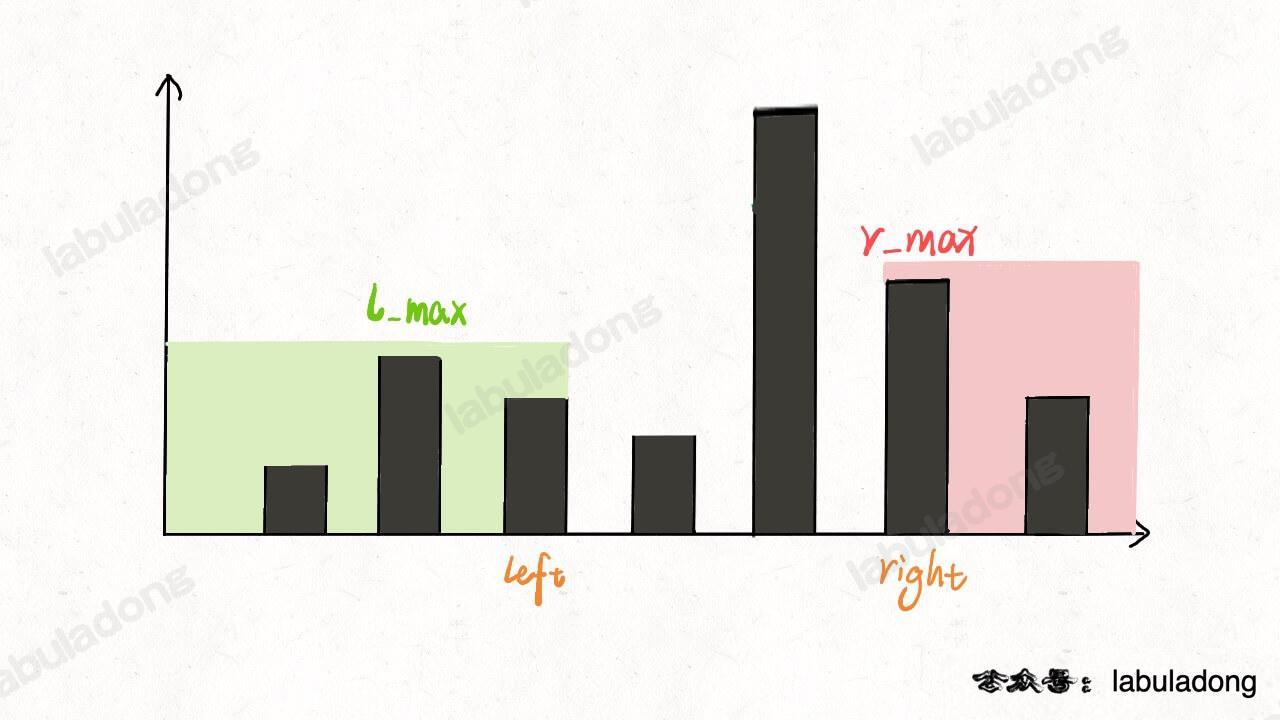
此时的 l_max 是 left 指针左边的最高柱子，但是 r_max 并不一定是 left 指针右边最高的柱子，这真的可以得到正确答案吗？

其实这个问题要这么思考，我们只在乎 min(l_max, r_max)。对于上图的情况，我们已经知道 l_max < r_max 了，至于这个 r_max 是不是右边最大的，不重要。重要的是 height[i] 能够装的水只和较低的 l_max 之差有关：

扩展延伸

题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例1：

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

思路

这题和接雨水问题很类似，可以完全套用前文的思路，而且还更简单。两道题的区别在于：

接雨水问题给出的类似一幅直方图，每个横坐标都有宽度，而本题给出的每个横坐标是一条竖线，没有宽度。

我们前文讨论了半天 l_max 和 r_max，实际上都是为了计算 height[i] 能够装多少水；而本题中 height[i] 没有了宽度，那自然就好办多了。

举个例子，如果在接雨水问题中，你知道了 height[left] 和 height[right] 的高度，你能算出 left 和 right 之间能够盛下多少水吗？

不能，因为你不知道 left 和 right 之间每个柱子具体能盛多少水，你得通过每个柱子的 l_max 和 r_max 来计算才行。

反过来，就本题而言，你知道了 height[left] 和 height[right] 的高度，能算出 left 和 right 之间能够盛下多少水吗？

可以，因为本题中竖线没有宽度，所以 left 和 right 之间能够盛的水就是：

min(height[left], height[right]) * (right - left)

类似接雨水问题，高度是由 height[left] 和 height[right] 较小的值决定的。

解决这道题的思路依然是双指针技巧：

用 left 和 right 两个指针从两端向中心收缩，一边收缩一边计算 [left, right] 之间的矩形面积，取最大的面积值即是答案。

先直接看解法代码吧：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0, right = height.size() - 1;
        int res = 0;
        while (left < right) {
            // [left, right] 之间的矩形面积
            int cur_area = min(height[left], height[right]) * (right - left);
            res = max(res, cur_area);
            // 双指针技巧，移动较低的一边
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        return res;
    }
};

代码和接雨水问题大致相同，不过肯定有读者会问，下面这段 if 语句为什么要移动较低的一边：

// 双指针技巧，移动较低的一边
if (height[left] < height[right]) {
    left++;
} else {
    right--;
}

其实也好理解，因为矩形的高度是由 min(height[left], height[right]) 即较低的一边决定的：

你如果移动较低的那一边，那条边可能会变高，使得矩形的高度变大，进而就「有可能」使得矩形的面积变大；相反，如果你去移动较高的那一边，矩形的高度是无论如何都不会变大的，所以不可能使矩形的面积变得更大。

括号相关问题

判断有效括号串

题目

输入一个字符串，其中包含 [](){} 六种括号，请你判断这个字符串组成的括号是否有效。

思路

举几个例子：

Input: "()[]{}"
Output: true

Input: "([)]"
Output: false

Input: "{[]}"
Output: true

解决这个问题之前，我们先降低难度，思考一下，如果只有一种括号 ()，应该如何判断字符串组成的括号是否有效呢？

假设字符串中只有圆括号，如果想让括号字符串有效，那么必须做到：

每个右括号 ) 的左边必须有一个左括号 ( 和它匹配。

比如说字符串 ()))(( 中，中间的两个右括号左边就没有左括号匹配，所以这个括号组合是无效的。

那么根据这个思路，我们可以写出算法：

bool isValid(std::string str) {
    // 待匹配的左括号数量
    int left = 0;
    for (int i = 0; i < str.size(); i++) {
        if (str[i] == '(') {
            left++;
        } else {
            // 遇到右括号
            left--;
        }

        // 右括号太多
        if (left == -1)
            return false;
    }
    // 是否所有的左括号都被匹配了
    return left == 0;
}

如果只有圆括号，这样就能正确判断有效性。对于三种括号的情况，我一开始想模仿这个思路，定义三个变量 left1，left2，left3 分别处理每种括号，虽然要多写不少 if else 分支，但是似乎可以解决问题。

但实际上直接照搬这种思路是不行的，比如说只有一个括号的情况下 (()) 是有效的，但是多种括号的情况下， [(]) 显然是无效的。

仅仅记录每种左括号出现的次数已经不能做出正确判断了，我们要加大存储的信息量，可以利用栈来模仿类似的思路。栈是一种先进后出的数据结构，处理括号问题的时候尤其有用。

我们这道题就用一个名为 left 的栈代替之前思路中的 left 变量，遇到左括号就入栈，遇到右括号就去栈中寻找最近的左括号，看是否匹配：

bool isValid(string str) {
    stack<char> left;
    for (char c : str) {
        if (c == '(' || c == '{' || c == '[') {
            left.push(c);
        } else { // 字符 c 是右括号
            if (!left.empty() && leftOf(c) == left.top()) {
                left.pop();
            } else {
                // 和最近的左括号不匹配
                return false;
            }
        }
    }
    // 是否所有的左括号都被匹配了
    return left.empty();
}

char leftOf(char c) {
    if (c == '}') return '{';
    if (c == ')') return '(';
    return '[';
}

平衡括号串（一）

题目

给你输入一个字符串 s，你可以在其中的任意位置插入左括号 ( 或者右括号 )，请问你最少需要几次插入才能使得 s 变成一个有效的括号串？

比如说输入 s = "())("，算法应该返回 2，因为我们至少需要插入两次把 s 变成 "(())()"，这样每个左括号都有一个右括号匹配，s 是一个有效的括号串。

这其实和前文的判断括号有效性非常类似，直接看代码：

class Solution {
public:
    int minAddToMakeValid(string s) {
        // res 记录插入次数
        int res = 0;
        // need 变量记录右括号的需求量
        int need = 0;

        for (int i = 0; i < s.size(); i++) {
            if (s[i] == '(') {
                // 对右括号的需求 + 1
                need++;
            }

            if (s[i] == ')') {
                // 对右括号的需求 - 1
                need--;

                if (need == -1) {
                    need = 0;
                    // 需插入一个左括号
                    res++;
                }
            }
        }

        return res + need;
    }
};

这段代码就是最终解法，核心思路是以左括号为基准，通过维护对右括号的需求数 need，来计算最小的插入次数。需要注意两个地方：

1、当 need == -1 的时候意味着什么？

因为只有遇到右括号 ) 的时候才会 need--，need == -1 意味着右括号太多了，所以需要插入左括号。

比如说 s = "))" 这种情况，需要插入 2 个左括号，使得 s 变成 "()()"，才是一个有效括号串。

2、算法为什么返回 res + need？

因为 res 记录的左括号的插入次数，need 记录了右括号的需求，当 for 循环结束后，若 need 不为 0，那么就意味着右括号还不够，需要插入。

比如说 s = "))(" 这种情况，插入 2 个左括号之后，还要再插入 1 个右括号，使得 s 变成 "()()()"，才是一个有效括号串。

以上就是这道题的思路，接下来我们看一道进阶题目，如果左右括号不是 1:1 配对，会出现什么问题呢？

平衡括号串（二）

题目

现在假设 1 个左括号需要匹配 2 个右括号才叫做有效的括号组合，那么给你输入一个括号串 s，请问你如何计算使得 s 有效的最小插入次数呢？

思路

核心思路还是和刚才一样，通过一个 need 变量记录对右括号的需求数，根据 need 的变化来判断是否需要插入。

第一步，我们按照刚才的思路正确维护 need 变量：

int minInsertions(std::string s) {
    // need 记录需右括号的需求量
    int res = 0, need = 0;
    for (int i = 0; i < s.size(); i++) {
        // 一个左括号对应两个右括号
        if (s[i] == '(') {
            need += 2;
        }

        if (s[i] == ')') {
            need--;
        }
    }
    return res + need;
}

现在想一想，当 need 为什么值的时候，我们可以确定需要进行插入？

首先，类似第一题，当 need == -1 时，意味着我们遇到一个多余的右括号，显然需要插入一个左括号。

比如说当 s = ")"，我们肯定需要插入一个左括号让 s = "()"，但是由于一个左括号需要两个右括号，所以对右括号的需求量变为 1：

if (s[i] == ')') {
    need--;
    // 说明右括号太多了
    if (need == -1) {
        // 需要插入一个左括号
        res++;
        // 同时，对右括号的需求变为 1
        need = 1;
    }
}

另外，当遇到左括号时，若对右括号的需求量为奇数，需要插入 1 个右括号。因为一个左括号需要两个右括号嘛，右括号的需求必须是偶数，这一点也是本题的难点。

所以遇到左括号时要做如下判断：

if (s[i] == '(') {
    need += 2;
    if (need % 2 == 1) {
        // 插入一个右括号
        res++;
        // 对右括号的需求减一
        need--;
    }
}

综上，我们可以写出正确的代码：

class Solution {
public:
    int minInsertions(string s) {
        int res = 0, need = 0;
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == '(') {
                need += 2;
                if (need % 2 == 1) {
                    res++;
                    need--;
                }
            }

            if (s[i] == ')') {
                need--;
                if (need == -1) {
                    res++;
                    need = 1;
                }
            }
        }
        return res + need;
    }
};

判定完美矩形

一个矩形有四个顶点，但是只要两个顶点的坐标就可以确定一个矩形了（比如左下角和右上角两个顶点坐标）。

题目

题目会给我们输入一个数组 rectangles，里面装着若干四元组 (x1,y1,x2,y2)，每个四元组就是记录一个矩形的左下角和右上角坐标。

也就是说，输入的 rectangles 数组实际上就是很多小矩形，题目要求我们输出一个布尔值，判断这些小矩形能否构成一个「完美矩形」。函数签名如下：

bool isRectangleCover(vector<vector<int>>& rectangles)

所谓「完美矩形」，就是说 rectangles 中的小矩形拼成图形必须是一个大矩形，且大矩形中不能有重叠和空缺。

比如说题目给我们举了几个例子：

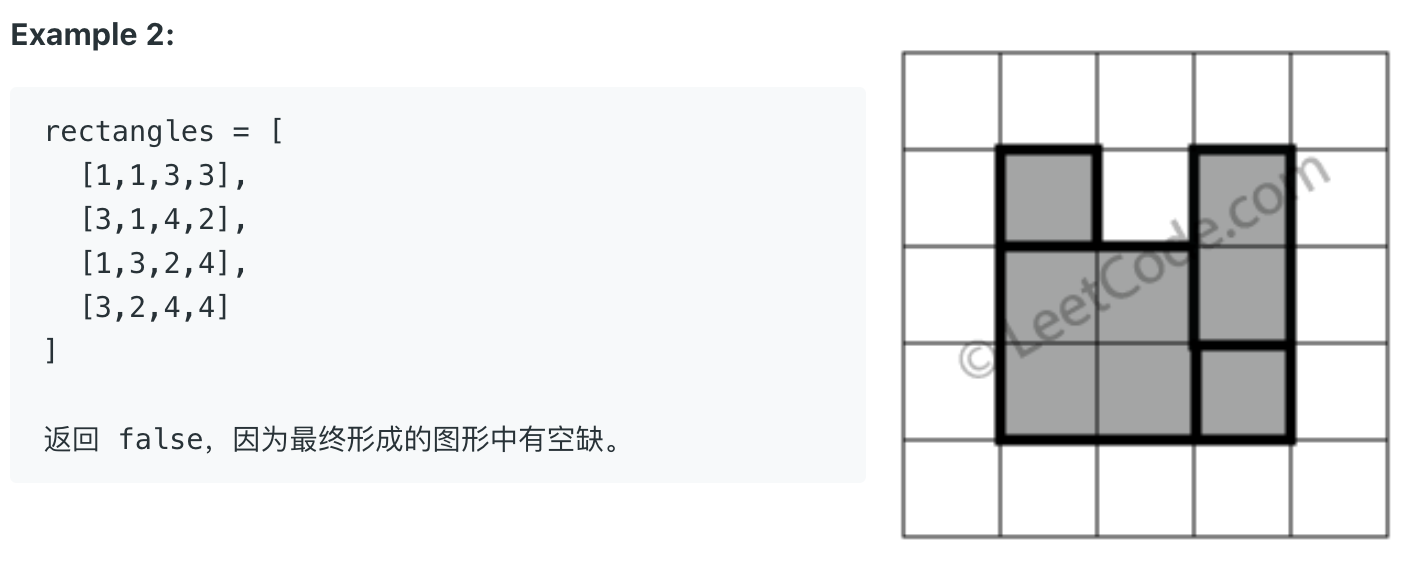
这个题目难度是 Hard，如果没有做过类似的题目，还真做不出来。

常规的思路，起码要把最终形成的图形表示出来吧，而且你要有方法去判断两个矩形是否有重叠，是否有空隙，虽然可以做到，不过感觉异常复杂。

其实，想判断最终形成的图形是否是完美矩形，需要从「面积」和「顶点」两个角度来处理。

先说说什么叫从「面积」的角度。

rectangles 数组中每个元素都是一个四元组 (x1, y1, x2, y2)，表示一个小矩形的左下角顶点坐标和右上角顶点坐标。

那么假设这些小矩形最终形成了一个「完美矩形」，你会不会求这个完美矩形的左下角顶点坐标 (X1, Y1) 和右上角顶点的坐标 (X2, Y2)？

这个很简单吧，左下角顶点 (X1, Y1) 就是 rectangles 中所有小矩形中最靠左下角的那个小矩形的左下角顶点；右上角顶点 (X2, Y2) 就是所有小矩形中最靠右上角的那个小矩形的右上角顶点。

注意我们用小写字母表示小矩形的坐标，大写字母表示最终形成的完美矩形的坐标，可以这样写代码：

// 左下角顶点，初始化为正无穷，以便记录最小值
int X1 = INT_MAX, Y1 = INT_MAX;
// 右上角顶点，初始化为负无穷，以便记录最大值
int X2 = INT_MIN, Y2 = INT_MIN;

for(auto &rectangle : rectangles) {
    int x1 = rectangle[0], y1 = rectangle[1], x2 = rectangle[2], y2 = rectangle[3];
    // 取小矩形左下角顶点的最小值
    X1 = min(X1, x1); Y1 = min(Y1, y1);
    // 取小矩形右上角顶点的最大值
    X2 = max(X2, x2); Y2 = max(Y2, y2);
}

这样就能求出完美矩形的左下角顶点坐标 (X1, Y1) 和右上角顶点的坐标 (X2, Y2) 了。

计算出的 X1,Y1,X2,Y2 坐标是完美矩形的「理论坐标」，如果所有小矩形的面积之和不等于这个完美矩形的理论面积，那么说明最终形成的图形肯定存在空缺或者重叠，肯定不是完美矩形。

代码可以进一步：

bool isRectangleCover(vector<vector<int>>& rectangles) {
    int X1 = numeric_limits<int>::max(), Y1 = numeric_limits<int>::max();
    int X2 = numeric_limits<int>::min(), Y2 = numeric_limits<int>::min();
    // 记录所有小矩形的面积之和
    int actualArea = 0;
    for (vector<int>& rect : rectangles) {
        int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        // 计算完美矩形的理论坐标
        X1 = min(X1, x1);
        Y1 = min(Y1, y1);
        X2 = max(X2, x2);
        Y2 = max(Y2, y2);
        // 累加所有小矩形的面积
        actualArea += (x2 - x1) * (y2 - y1);
    }

    // 计算完美矩形的理论面积
    int expectedArea = (X2 - X1) * (Y2 - Y1);
    // 面积应该相同
    if (actualArea != expectedArea) {
        return false;
    }

    return true;
}

这样，「面积」这个维度就完成了，思路其实不难，无非就是假设最终形成的图形是个完美矩形，然后比较面积是否相等，如果不相等的话说明最终形成的图形一定存在空缺或者重叠部分，不是完美矩形。

但是反过来说，如果面积相同，是否可以证明最终形成的图形是完美矩形，一定不存在空缺或者重叠？

肯定是不行的，举个很简单的例子，你假想一个完美矩形，然后我在它中间挖掉一个小矩形，把这个小矩形向下平移一个单位。这样小矩形的面积之和没变，但是原来的完美矩形中就空缺了一部分，也重叠了一部分，已经不是完美矩形了。

综上，即便面积相同，并不能完全保证不存在空缺或者重叠，所以我们需要从「顶点」的维度来辅助判断。

记得小学的时候有一道智力题，给你一个矩形，切一刀，剩下的图形有几个顶点？答案是，如果沿着对角线切，就剩 3 个顶点；如果横着或者竖着切，剩 4 个顶点；如果只切掉一个小角，那么会出现 5 个顶点。

回到这道题，我们接下来的分析也有那么一点智力题的味道。

显然，完美矩形一定只有四个顶点。矩形嘛，按理说应该有四个顶点，如果存在空缺或者重叠的话，肯定不是四个顶点，比如说题目的这两个例子就有不止 4 个顶点：

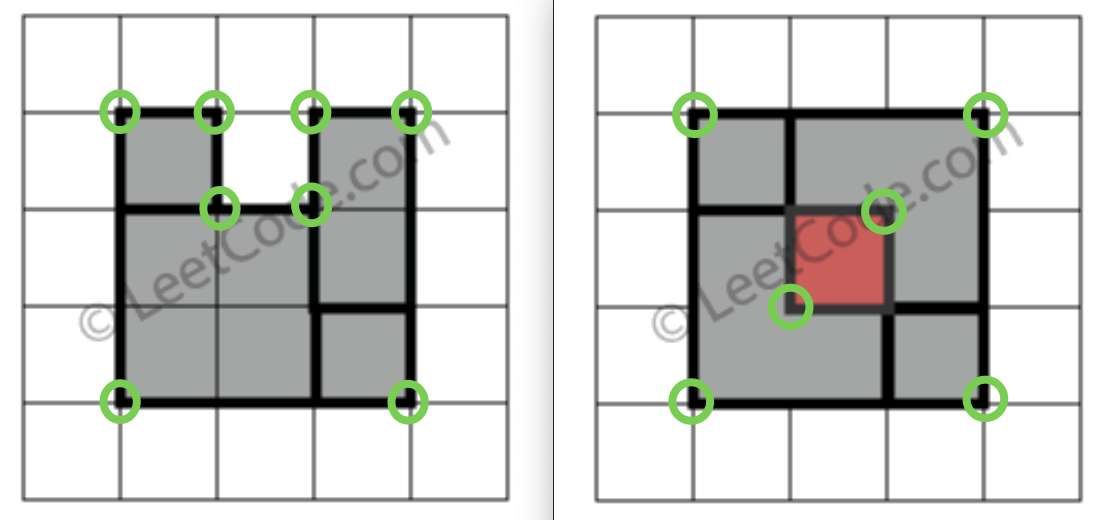
只要我们想办法计算 rectangles 中的小矩形最终形成的图形有几个顶点，就能判断最终的图形是不是一个完美矩形了。

那么顶点是如何形成的呢？我们倒是一眼就可以看出来顶点在哪里，问题是如何让计算机，让算法知道某一个点是不是顶点呢？这也是本题的难点所在。

看下图的四种情况：

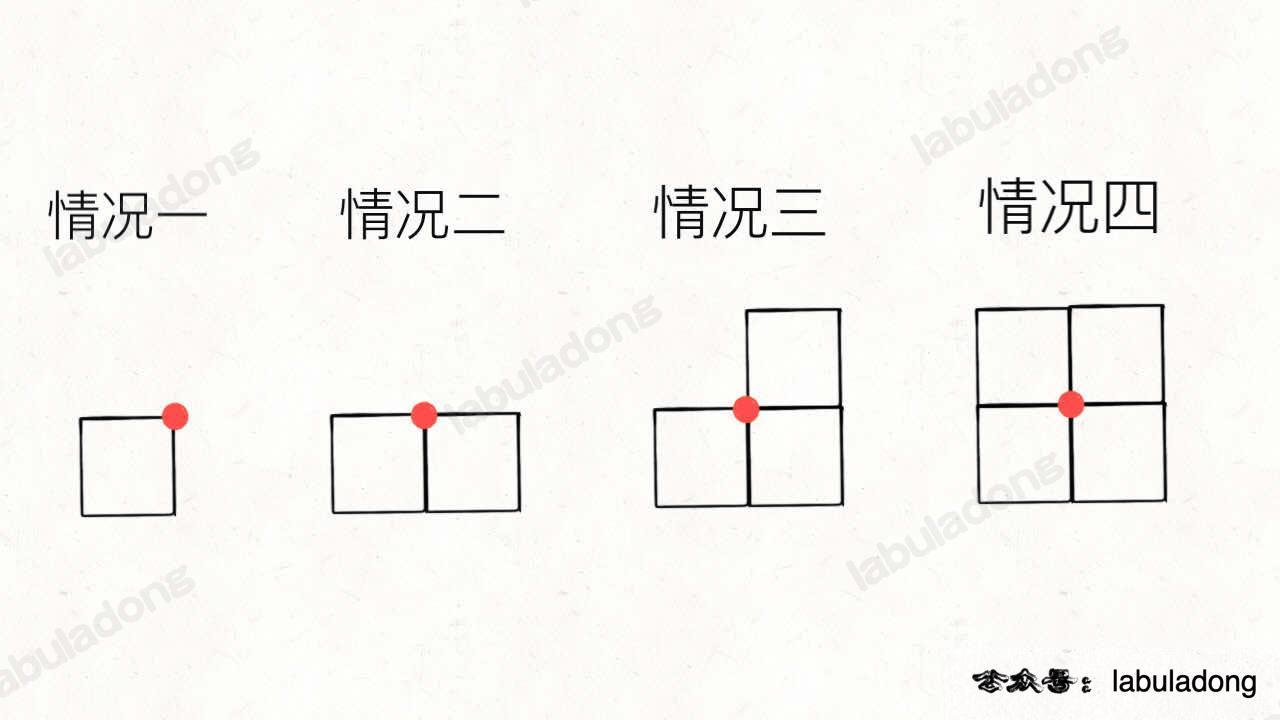
图中画红点的地方，什么时候是顶点，什么时候不是顶点？显然，情况一和情况三的时候是顶点，而情况二和情况四的时候不是顶点。

也就是说，当某一个点同时是 2 个或者 4 个小矩形的顶点时，该点最终不是顶点；当某一个点同时是 1 个或者 3 个小矩形的顶点时，该点最终是一个顶点。

注意，2 和 4 都是偶数，1 和 3 都是奇数，我们想计算最终形成的图形中有几个顶点，也就是要筛选出那些出现了奇数次的顶点，可以这样写代码：

bool isRectangleCover(vector<vector<int>>& rectangles) {
    int X1 = INT_MAX, Y1 = INT_MAX;
    int X2 = INT_MIN, Y2 = INT_MIN;
    
    int actualArea = 0;
    // 哈希集合，记录最终图形的顶点
    unordered_set<string> points;
    
    for (const auto& rect : rectangles) {
        int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        
        X1 = min(X1, x1);
        Y1 = min(Y1, y1);
        X2 = max(X2, x2);
        Y2 = max(Y2, y2);

        actualArea += (x2 - x1) * (y2 - y1);
        
        // 先算出小矩形每个点的坐标，用字符串表示，方便存入哈希集合
        string p1 = to_string(x1) + "," + to_string(y1);
        string p2 = to_string(x1) + "," + to_string(y2);
        string p3 = to_string(x2) + "," + to_string(y1);
        string p4 = to_string(x2) + "," + to_string(y2);
        
        // 对于每个点，如果存在集合中，删除它；如果不存在集合中，添加它；在集合中剩下的点都是出现奇数次的点
        for (const string& p : {p1, p2, p3, p4}) {
            if (points.count(p)) {  // 在加上这个点就是偶数次
                points.erase(p);
            }
            else {
                points.insert(p);  // 加上这个点就是奇数次
            }
        }
    }
    
    int expectedArea = (X2 - X1) * (Y2 - Y1);
    if (actualArea != expectedArea) {
        return false;
    }
    
    // 检查顶点个数
    if (points.size() != 4 || 
        !points.count(to_string(X1) + "," + to_string(Y1)) || 
        !points.count(to_string(X1) + "," + to_string(Y2)) || 
        !points.count(to_string(X2) + "," + to_string(Y1)) || 
        !points.count(to_string(X2) + "," + to_string(Y2))) {
        return false;
    }
    
    return true;
}

这段代码中，我们用一个 points 集合记录 rectangles 中小矩形组成的最终图形的顶点坐标，关键逻辑在于如何向 points 中添加坐标：

如果某一个顶点 p 存在于集合 points 中，则将它删除；如果不存在于集合 points 中，则将它插入。

这个简单的逻辑，让 points 集合最终只会留下那些出现了 1 次或者 3 次的顶点，那些出现了 2 次或者 4 次的顶点都被消掉了。

那么首先想到，points 集合中最后应该只有 4 个顶点对吧，如果 len(points) != 4 说明最终构成的图形肯定不是完美矩形。

但是如果 len(points) == 4 是否能说明最终构成的图形肯定是完美矩形呢？也不行，因为题目并没有说 rectangles 中的小矩形不存在重复，比如下面这种情况：

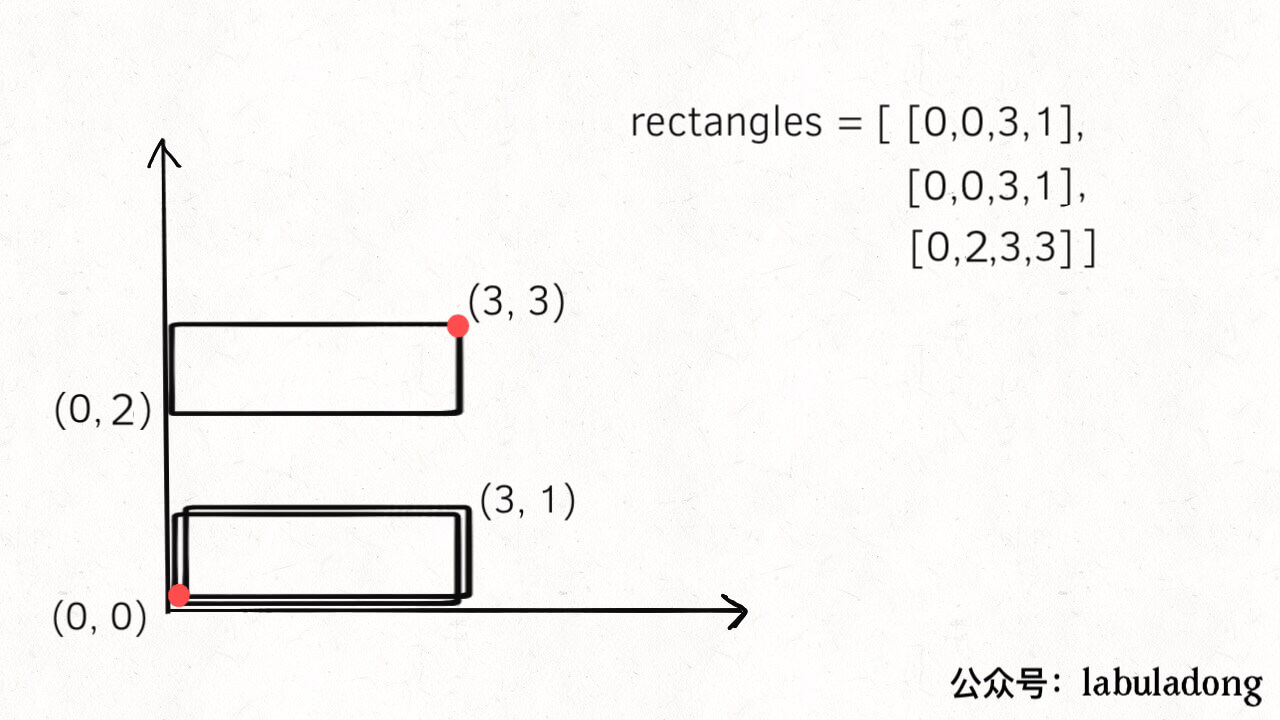
下面两个矩形重复了，按照我们的算法逻辑，它们的顶点都被消掉了，最终是剩下了四个顶点；再看面积，完美矩形的理论坐标是图中红色的点，计算出的理论面积和实际面积也相同。但是显然这种情况不是题目要求完美矩形。

所以不仅要保证 len(points) == 4，而且要保证 points 中最终剩下的点坐标就是完美矩形的四个理论坐标，直接看代码吧：

class Solution {
public:
    bool isRectangleCover(vector<vector<int>>& rectangles) {
        int X1 = INT_MAX, Y1 = INT_MAX;
        int X2 = INT_MIN, Y2 = INT_MIN;
        
        set<string> points;
        int actualArea = 0;
        
        for (auto & rect : rectangles) {
            int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
            // 计算完美矩形的理论顶点坐标
            X1 = min(X1, x1);
            Y1 = min(Y1, y1);
            X2 = max(X2, x2);
            Y2 = max(Y2, y2);
            // 累加小矩形的面积
            actualArea += (x2 - x1) * (y2 - y1);
            // 记录最终形成的图形中的顶点
            string p1 = to_string(x1) + "," + to_string(y1);
            string p2 = to_string(x1) + "," + to_string(y2);
            string p3 = to_string(x2) + "," + to_string(y1);
            string p4 = to_string(x2) + "," + to_string(y2);
            for (string p : {p1, p2, p3, p4}) {
                if (points.count(p)) {
                    points.erase(p);
                } else {
                    points.insert(p);
                }
            }
        }
        // 判断面积是否相同
        int expectedArea = (X2 - X1) * (Y2 - Y1);
        if (actualArea != expectedArea) {
            return false;
        }
        // 判断最终留下的顶点个数是否为 4
        if (points.size() != 4) {
            return false;
        }
        // 判断留下的 4 个顶点是否是完美矩形的顶点
        if (!points.count(to_string(X1) + "," + to_string(Y1))) return false;
        if (!points.count(to_string(X1) + "," + to_string(Y2))) return false;
        if (!points.count(to_string(X2) + "," + to_string(Y1))) return false;
        if (!points.count(to_string(X2) + "," + to_string(Y2))) return false;
        // 面积和顶点都对应，说明矩形符合题意
        return true;
    }
};

这就是最终的解法代码，从「面积」和「顶点」两个维度来判断：

1、判断面积，通过完美矩形的理论坐标计算出一个理论面积，然后和 rectangles 中小矩形的实际面积和做对比。

2、判断顶点，points 集合中应该只剩下 4 个顶点且剩下的顶点必须都是完美矩形的理论顶点。