题目:
给你一个长度为 n 的 正 整数数组 nums 。
如果两个 非负 整数数组 (arr1, arr2) 满足以下条件,我们称它们是 单调 数组对:
- 两个数组的长度都是
n。 arr1是单调 非递减 的,换句话说arr1[0] <= arr1[1] <= ... <= arr1[n - 1]。arr2是单调 非递增 的,换句话说arr2[0] >= arr2[1] >= ... >= arr2[n - 1]。- 对于所有的
0 <= i <= n - 1都有arr1[i] + arr2[i] == nums[i]。
请你返回所有 单调 数组对的数目。
由于答案可能很大,请你将它对 109 + 7 取余 后返回。
示例 1:
输入:nums = [2,3,2]
输出:4
解释:
单调数组对包括:
([0, 1, 1], [2, 2, 1])([0, 1, 2], [2, 2, 0])([0, 2, 2], [2, 1, 0])([1, 2, 2], [1, 1, 0])
示例 2:
输入:nums = [5,5,5,5]
输出:126
提示:
1 <= n == nums.length <= 20001 <= nums[i] <= 50
思路:
哈?
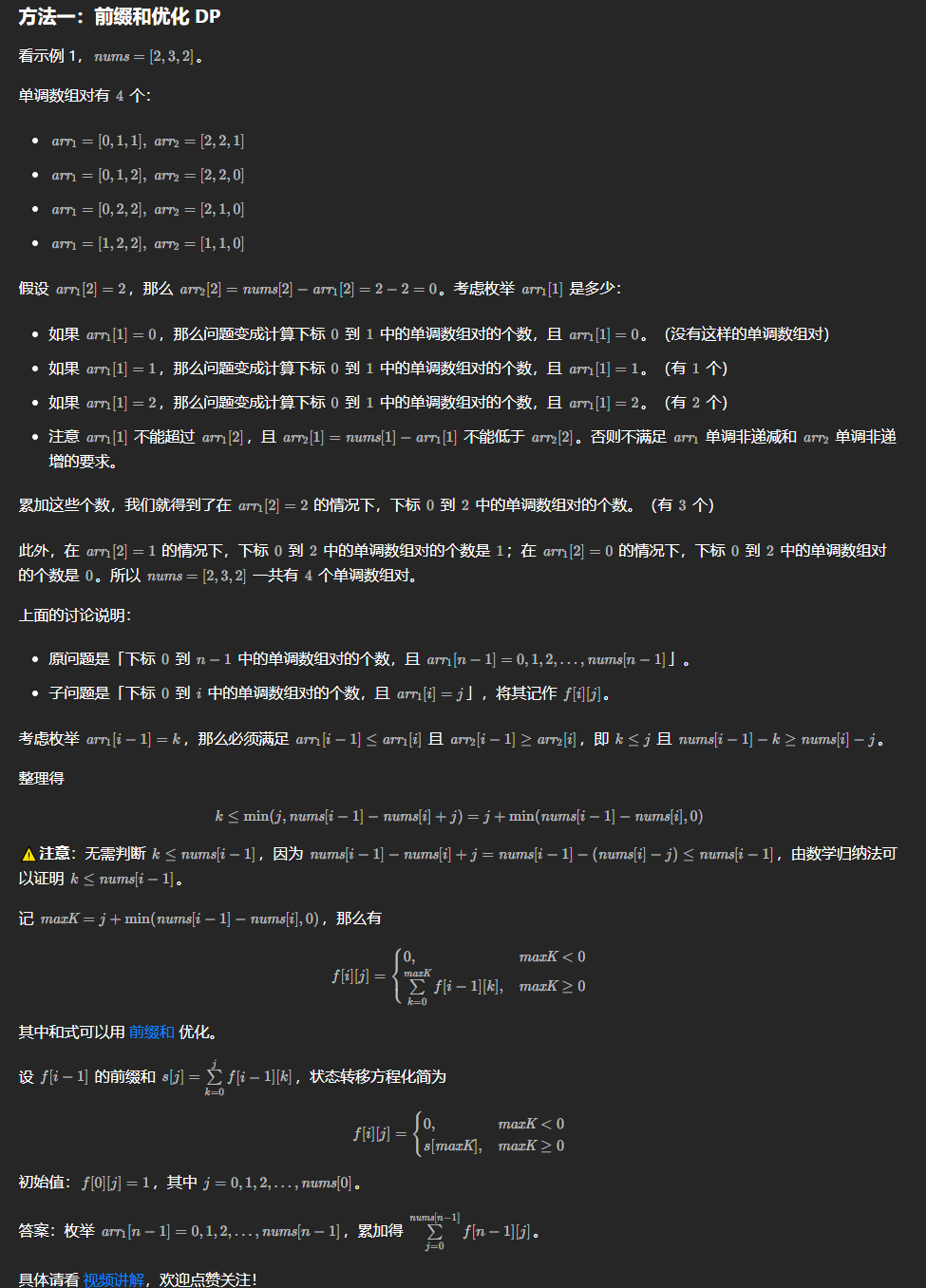
代码:
class Solution {
public:
int countOfPairs(vector<int>& nums) {
const int MOD = 1'000'000'007;
int n = nums.size();
int m = ranges::max(nums);
vector f(n, vector<long long>(m + 1));
vector<long long> s(m + 1);
fill(f[0].begin(), f[0].begin() + nums[0] + 1, 1);
for (int i = 1; i < n; i++) {
partial_sum(f[i - 1].begin(), f[i - 1].end(), s.begin()); // f[i-1] 的前缀和
for (int j = 0; j <= nums[i]; j++) {
int max_k = j + min(nums[i - 1] - nums[i], 0);
f[i][j] = max_k >= 0 ? s[max_k] % MOD : 0;
}
}
return reduce(f[n - 1].begin(), f[n - 1].begin() + nums[n - 1] + 1, 0LL) % MOD;
}
};