题目:
给你一个 m x n 的二进制矩阵 grid 。
如果矩阵中一行或者一列从前往后与从后往前读是一样的,那么我们称这一行或者这一列是 回文 的。
你可以将 grid 中任意格子的值 翻转 ,也就是将格子里的值从 0 变成 1 ,或者从 1 变成 0 。
请你返回 最少 翻转次数,使得矩阵中 所有 行和列都是 回文的 ,且矩阵中 1 的数目可以被 4 整除 。
示例 1:
输入:grid = [[1,0,0],[0,1,0],[0,0,1]]
输出:3
解释:

示例 2:
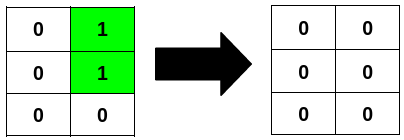
输入:grid = [[0,1],[0,1],[0,0]]
输出:2
解释:
示例 3:
输入:grid = [[1],[1]]
输出:2
解释:

提示:
m == grid.lengthn == grid[i].length1 <= m * n <= 2 * 1050 <= grid[i][j] <= 1
思路:
分析:行和列都是回文
为方便描述,把 grid 简称为 a。
由于所有行和列都必须是回文的,所以要满足
a[i][j] = a[i][n−1−j] = a[m−1−i][j] = a[m−1−i][n−1−j]
也就是这四个数要么都是 0,要么都是 1。其中 0 ≤ i ≤ ⌊m/2⌋, 0 ≤ j ≤ ⌊n/2⌋。
设 cnt1 = a[i][j] + a[i][n−1−j] + a[m−1−i][j] + a[m−1−i][n−1−j]
把这四个数都变成 0 需要翻转 cnt1 次,都变成 1 需要翻转 4 − cnt1 次。
两种情况取最小值,把 min(cnt1, 4 − cnt1) 加入答案。
分析:1 的数目被 4 整除
分类讨论:
如果 m 和 n 都是偶数:由于上面四个数四个数一组,都翻转成了 0 或者 1,所以 1 的数目能被 4 整除自动成立。
如果 m 是奇数,n 是偶数:正中间一排需要翻转成回文的,且 1 的数目需要能被 4 整除。
如果 m 是偶数,n 是奇数:正中间一列需要翻转成回文的,且 1 的数目需要能被 4 整除。
如果 m 和 n 都是奇数:正中间一排和正中间一列都需要翻转成回文的,且 1 的数目需要能被 4 整除。除了正中央的格子以外,每个格子都有镜像位置,这些格子两个数两个数一组,都翻转成了 0 或者 1。那么翻转之后,不考虑正中央的格子,1 的数目就是偶数。所以正中央的格子必须是 0,否则最终 1 的数目是奇数,无法被 4 整除。
如何处理正中间一排和正中间一列,是本题的重点。
具体计算方法
首先,如果 m 和 n 都是奇数,那么正中央的格子 (⌊m/2⌋, ⌊n/2⌋) 必须是 0,把其元素值加入答案。
然后统计正中间一排(如果 m 是奇数)和正中间一列(如果 n 是奇数)的格子:
设 diff 为镜像位置不同的数对个数。注意统计的是数对。
设 cnt1 为镜像位置相同的 1 的个数。注意统计的是个数。
这 diff 对 0 和 1 必须翻转其中一个数,所以答案至少要增加 diff。什么情况下,可以只增加 diff?
分类讨论:
如果 cnt1 是 4 的倍数,那么只需把这 diff 对 0 和 1 中的 1 全部变成 0,这样 1 的个数就是 4 的倍数了。所以把 diff 加入答案。
如果 cnt1 不是 4 的倍数,由于 cnt1 是偶数,其除以 4 必定余 2(注意这说明 cnt1 ≥ 2)。继续讨论:
如果 diff > 0,把其中一对数都变成 1,其余 diff−1 对数全部变成 0,这样 1 的个数就是 4 的倍数了。所以同样地,把 diff 加入答案。
如果 diff = 0,我们只能把 cnt1 中的两个 1 变成 0,使得 1 的个数是 4 的倍数。所以把答案增加 2。
综上所述:
如果 diff > 0,额外把 diff 加入答案。
如果 diff = 0,额外把 cnt1 mod 4 加入答案。
代码:
class Solution {
public:
int minFlips(vector<vector<int>>& a) {
int m = a.size(), n = a[0].size();
int ans = 0;
for (int i = 0; i < m / 2; i++) {
for (int j = 0; j < n / 2; j++) {
int cnt1 = a[i][j] + a[i][n - 1 - j] + a[m - 1 - i][j] + a[m - 1 - i][n - 1 - j];
ans += min(cnt1, 4 - cnt1); // 全为 1 或全为 0
}
}
if (m % 2 && n % 2) {
// 正中间的数必须是 0
ans += a[m / 2][n / 2];
}
int diff = 0, cnt1 = 0;
if (m % 2) {
// 统计正中间这一排
for (int j = 0; j < n / 2; j++) {
if (a[m / 2][j] != a[m / 2][n - 1 - j]) {
diff++;
} else {
cnt1 += a[m / 2][j] * 2;
}
}
}
if (n % 2) {
// 统计正中间这一列
for (int i = 0; i < m / 2; i++) {
if (a[i][n / 2] != a[m - 1 - i][n / 2]) {
diff++;
} else {
cnt1 += a[i][n / 2] * 2;
}
}
}
return ans + (diff ? diff : cnt1 % 4);
}
};