题目:
给你两个正整数 xCorner 和 yCorner 和一个二维整数数组 circles ,其中 circles[i] = [xi, yi, ri] 表示一个圆心在 (xi, yi) 半径为 ri 的圆。
坐标平面内有一个左下角在原点,右上角在 (xCorner, yCorner) 的矩形。你需要判断是否存在一条从左下角到右上角的路径满足:路径 完全 在矩形内部,不会 触碰或者经过 任何 圆的内部和边界,同时 只 在起点和终点接触到矩形。
如果存在这样的路径,请你返回 true ,否则返回 false 。
示例 1:
输入:X = 3, Y = 4, circles = [[2,1,1]]
输出:true
解释:
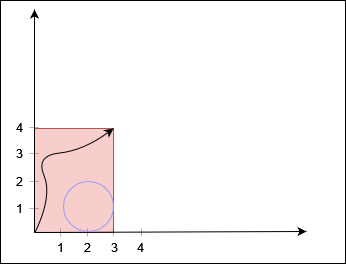
黑色曲线表示一条从 (0, 0) 到 (3, 4) 的路径。
示例 2:
输入:X = 3, Y = 3, circles = [[1,1,2]]
输出:false
解释:
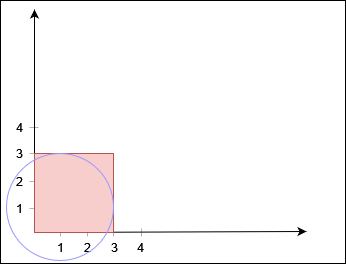
不存在从 (0, 0) 到 (3, 3) 的路径。
示例 3:
输入:X = 3, Y = 3, circles = [[2,1,1],[1,2,1]]
输出:false
解释:
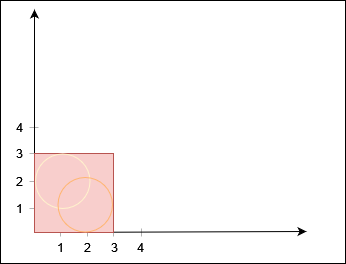
不存在从 (0, 0) 到 (3, 3) 的路径。
示例 4:
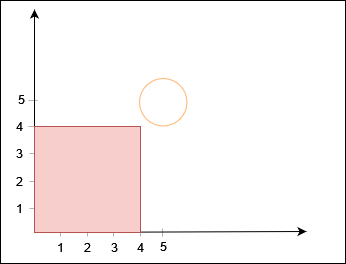
输入:X = 4, Y = 4, circles = [[5,5,1]]
输出:true
解释:
提示:
3 <= xCorner, yCorner <= 1091 <= circles.length <= 1000circles[i].length == 31 <= xi, yi, ri <= 109
思路:
这题有点回忆起了高中做解析几何的感觉,真的很难。
关键在与数学建模出无向图,并计算怎么根据圆和矩形的关系来建边
如果从矩形【上边界/左边界】到矩形【右边界/下边界】的路被圆堵死,则无法从矩形左下角移动到矩形右上角。
怎么判断呢?
首先考虑圆心都在矩形内部的情况。如果圆和圆相交或相切,则相当于在两个圆之间架起了一座桥。如果圆和矩形边界相交或相切,则相当于在矩形边界和圆之间架起了一座桥。如果可以从矩形【上边界/左边界】通过桥到达矩形【右边界/下边界】,则说明路被堵死,无法从矩形左下角移动到矩形右上角。
也可以把桥理解成切割线,如果能把从矩形左下角到矩形右上角的路径切断,则无法从矩形左下角移动到矩形右上角。
用图论的术语来说,就是把圆抽象成节点,在相交或相切的节点之间连边,得到一张无向图。如果从与【上边界/左边界】相交的节点出发,DFS 这张图,到达与【右边界/下边界】相交的节点,则说明无法从矩形左下角移动到矩形右上角。
需要注意,本题没有保证圆心一定在矩形内部,如何处理这种情况呢?

注:把两圆的两个交点连起来,该线段与 O1O2 相交得到的交点作为点 A 也可以,但这种情况点 A 横纵坐标的分母会是一个 10^18 数量级的数,在与 X 或 Y 相乘时会产生 10^27 数量级的数,超出了 64 位整数的范围,需要用大整数实现,更麻烦。
如何判断圆是否与矩形边界相交相切?

具体做法 从与矩形【上边界/左边界】相交/相切的圆开始 DFS。
如果当前 DFS 到了圆 i:
-
先判断其是否与矩形【右边界/下边界】相交或相切,如果是,则 DFS 返回 true。
-
否则,判断其是否与其他圆 j 相交或相切,如果是,则判断点 A 是否严格在矩形内,如果在,则递归 j,如果收到了 true,则 DFS 返回 true。
最后,如果最外层调用 DFS 的地方收到了 true,则表示无法从矩形左下角移动到矩形右上角,返回 false。
代码实现时,可以在递归之前,特判圆包含矩形左下角或者矩形右上角的情况,此时可以直接返回 false。
代码:
class Solution {
// 判断点 (x,y) 是否在圆 (ox,oy,r) 内
bool in_circle(long long ox, long long oy, long long r, long long x, long long y) {
return (ox - x) * (ox - x) + (oy - y) * (oy - y) <= r * r;
}
public:
bool canReachCorner(int X, int Y, vector<vector<int>>& circles) {
int n = circles.size();
vector<int> vis(n);
auto dfs = [&](auto&& dfs, int i) -> bool {
long long x1 = circles[i][0], y1 = circles[i][1], r1 = circles[i][2];
// 圆 i 是否与矩形右边界/下边界相交相切
if (y1 <= Y && abs(x1 - X) <= r1 ||
x1 <= X && y1 <= r1 ||
x1 > X && in_circle(x1, y1, r1, X, 0)) {
return true;
}
vis[i] = true;
for (int j = 0; j < n; j++) {
long long x2 = circles[j][0], y2 = circles[j][1], r2 = circles[j][2];
// 在两圆相交相切的前提下,点 A 是否严格在矩形内
if (!vis[j] && (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) <= (r1 + r2) * (r1 + r2) &&
x1 * r2 + x2 * r1 < (r1 + r2) * X &&
y1 * r2 + y2 * r1 < (r1 + r2) * Y &&
dfs(dfs, j)) {
return true;
}
}
return false;
};
for (int i = 0; i < n; i++) {
long long x = circles[i][0], y = circles[i][1], r = circles[i][2];
if (in_circle(x, y, r, 0, 0) || // 圆 i 包含矩形左下角
in_circle(x, y, r, X, Y) || // 圆 i 包含矩形右上角
// 圆 i 是否与矩形上边界/左边界相交相切
!vis[i] && (x <= X && abs(y - Y) <= r ||
y <= Y && x <= r ||
y > Y && in_circle(x, y, r, 0, Y)) && dfs(dfs, i)) {
return false;
}
}
return true;
}
};