矩阵中的最大得分

2024-08-15

leetcode

题目：

给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格（不必相邻）。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。

你可以从任一单元格开始，并且必须至少移动一次。

返回你能得到的最大总得分。

示例 1：

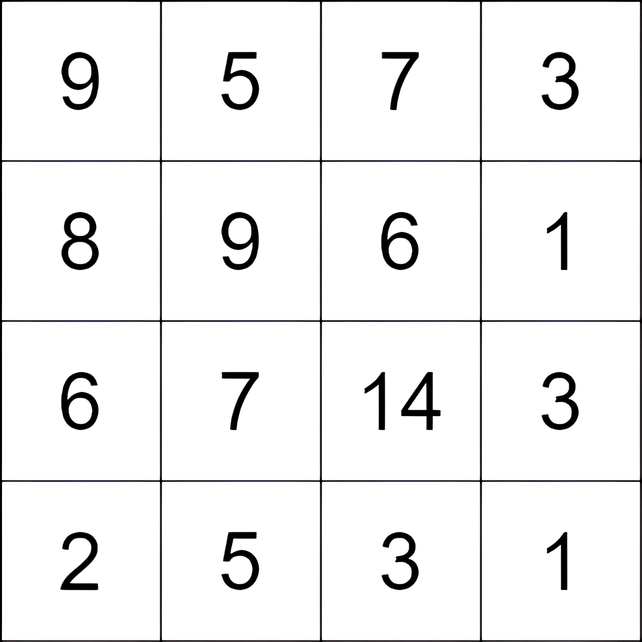
输入：grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]

输出：9

解释：从单元格 (0, 1) 开始，并执行以下移动： - 从单元格 (0, 1) 移动到 (2, 1)，得分为 7 - 5 = 2 。 - 从单元格 (2, 1) 移动到 (2, 2)，得分为 14 - 7 = 7 。总得分为 2 + 7 = 9 。

示例 2：

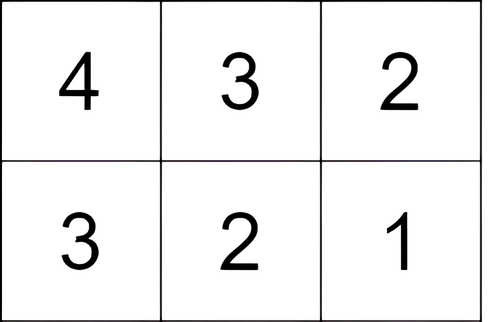
输入：grid = [[4,3,2],[3,2,1]]

输出：-1

解释：从单元格 (0, 0) 开始，执行一次移动：从 (0, 0) 到 (0, 1) 。得分为 3 - 4 = -1 。

提示：

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 105
1 <= grid[i][j] <= 105

思路：

// 思路：从正面想问题会非常难：
        // 主要原因就是最后答案开始的单元格不确定，同时路径也不确定，用代码刻画这个路径也很困难
        // 所以我们反过来想，如果我们已经最终的答案路径的单元格分数是 c1, c2, c3, c4
        // 那么得分就是 c4 - c3 + c3 - c2 + c2 - c1 = c4 - c1
        // 从这里就可以看出一个规律，任何一条路径得分 = 末尾点分数 - 起始点分数
        // 那么问题就转化成 从任一一点出发， 他能到达的所有点， 这些分数的最大值是多少。
        // 如果直接暴力求解，那么时间复杂度是 O(n^4) 
        // 从题目规定的可行路径来看，其实就是求某个数字右下方的数字的最大值
        // 这里就是动态规划可以插手的
        // 比如 grid[i][j] 右下方的最大值元素就是 grid[i+1][j] 和 grid[i][j+1] 右下方的最大值元素 中的最大值 （grid[i][j+1]、grid[i+1][j]也要比）

代码：

class Solution {
public:
    int maxScore(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        // 存在(i, j)可到达的点的最大值
        vector<vector<int>> dp(m, vector<int>(n));
        dp[m - 1][n - 1] = -1e5;  // 这里起始点的取值必须是非常小才行，因为不可能从这里出发的，但是为了将这个点纳入动态规划中，必须赋值
        for (int i = m - 1; i >= 0; i--) {
            for (int j = n - 1; j>= 0; j--) {
                if (i == m - 1 && j == n - 1) continue;
                if (i == m - 1) dp[i][j] = max(dp[i][j + 1], grid[i][j + 1]);
                else if (j == n - 1) dp[i][j] = max(dp[i + 1][j], grid[i + 1][j]);
                else {
                    dp[i][j] = max(grid[i + 1][j], max(
                        grid[i][j + 1], max(
                            dp[i + 1][j], dp[i][j + 1])
                        )
                    );
                }
            }
        }
        int ans = INT_MIN;
        // 枚举每个点作为起始点
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                ans = max(ans, dp[i][j] - grid[i][j]);
            }
        }
        return ans;
    }
};