题目:
在二维平面上的 x 轴上,放置着一些方块。
给你一个二维整数数组 positions ,其中 positions[i] = [lefti, sideLengthi] 表示:第 i 个方块边长为 sideLengthi ,其左侧边与 x 轴上坐标点 lefti 对齐。
每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落,直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆,它就会固定在原地,无法移动。
在每个方块掉落后,你必须记录目前所有已经落稳的 方块堆叠的最高高度 。
返回一个整数数组 ans ,其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。
示例 1:
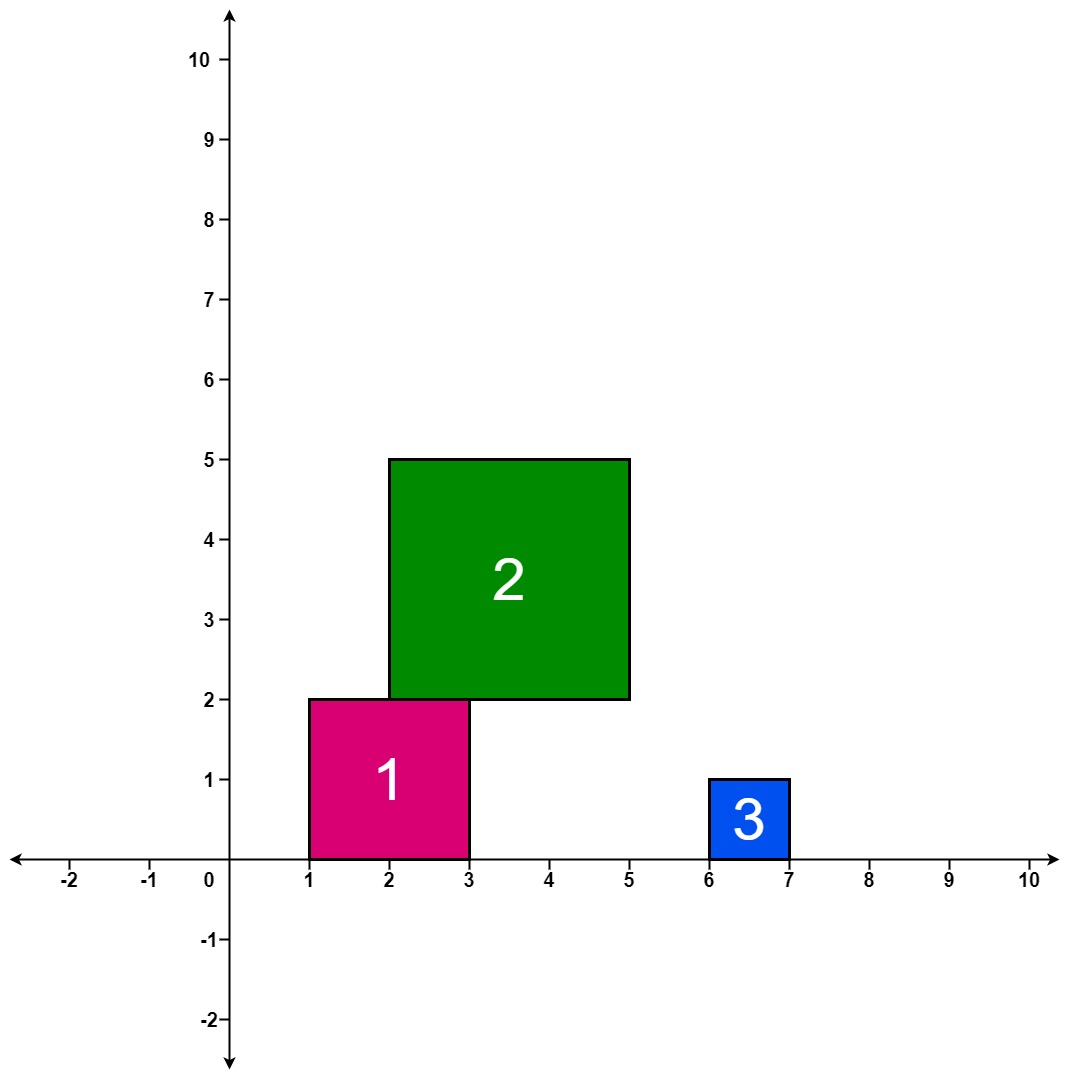
输入:positions = [[1,2],[2,3],[6,1]]
输出:[2,5,5]
解释:
第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 2 。
第 2 个方块掉落后,最高的堆叠由方块 1 和 2 组成,堆叠的最高高度为 5 。
第 3 个方块掉落后,最高的堆叠仍然由方块 1 和 2 组成,堆叠的最高高度为 5 。
因此,返回 [2, 5, 5] 作为答案。
示例 2:
输入:positions = [[100,100],[200,100]]
输出:[100,100]
解释:
第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 100 。
第 2 个方块掉落后,最高的堆叠可以由方块 1 组成也可以由方块 2 组成,堆叠的最高高度为 100 。
因此,返回 [100, 100] 作为答案。
注意,方块 2 擦过方块 1 的右侧边,但不会算作在方块 1 上着陆。
提示:
1 <= positions.length <= 10001 <= lefti <= 1081 <= sideLengthi <= 106
思路:
我们用数组 heights 记录各个方块掉落后的高度。对于第 i 个掉落的方块,如果它的底部区间与第 j 个掉落的方块有重叠,那么它掉落后的高度至少为 heights[j] + sizei,其中 j < i 且 sizei 为第 i 个掉落的方块的边长。因此对于第 i 个掉落的方块,heights[i] 的初始值为 sizei,我们暴力枚举所有之前已经掉落的方块,如果两者的底部区间有重叠,那么更新 heights[i] = max(heights[i], heights[j] + sizei)。
因为题目要求返回一个所有已经落稳的方块的最大堆叠高度列表,我们从 i = 1 开始,更新 heights[i] = max(heights[i], heights[i−1]),然后返回 heights 即可。
代码:
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
int n = positions.size();
vector<int> heights(n);
for (int i = 0; i < n; i++) {
int left1 = positions[i][0], right1 = positions[i][0] + positions[i][1] - 1;
heights[i] = positions[i][1];
for (int j = 0; j < i; j++) {
int left2 = positions[j][0], right2 = positions[j][0] + positions[j][1] - 1;
if (right1 >= left2 && right2 >= left1) {
heights[i] = max(heights[i], heights[j] + positions[i][1]);
}
}
}
for (int i = 1; i < n; i++) {
heights[i] = max(heights[i], heights[i - 1]);
}
return heights;
}
};