题目:
有一棵由 n 个节点组成的无向树,以 0 为根节点,节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维 整数 数组 edges ,其中 edges[i] = [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ,其中 coins[i] 表示节点 i 处的金币数量。
从根节点开始,你必须收集所有金币。要想收集节点上的金币,必须先收集该节点的祖先节点上的金币。
节点 i 上的金币可以用下述方法之一进行收集:
- 收集所有金币,得到共计
coins[i] - k点积分。如果coins[i] - k是负数,你将会失去abs(coins[i] - k)点积分。 - 收集所有金币,得到共计
floor(coins[i] / 2)点积分。如果采用这种方法,节点i子树中所有节点j的金币数coins[j]将会减少至floor(coins[j] / 2)。
返回收集 所有 树节点的金币之后可以获得的最大积分。
示例 1:

输入:edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5
输出:11
解释:
使用第一种方法收集节点 0 上的所有金币。总积分 = 10 - 5 = 5 。
使用第一种方法收集节点 1 上的所有金币。总积分 = 5 + (10 - 5) = 10 。
使用第二种方法收集节点 2 上的所有金币。所以节点 3 上的金币将会变为 floor(3 / 2) = 1 ,总积分 = 10 + floor(3 / 2) = 11 。
使用第二种方法收集节点 3 上的所有金币。总积分 = 11 + floor(1 / 2) = 11.
可以证明收集所有节点上的金币能获得的最大积分是 11 。
示例 2:
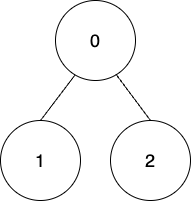
输入:edges = [[0,1],[0,2]], coins = [8,4,4], k = 0
输出:16
解释:
使用第一种方法收集所有节点上的金币,因此,总积分 = (8 - 0) + (4 - 0) + (4 - 0) = 16 。
提示:
n == coins.length2 <= n <= 1050 <= coins[i] <= 104edges.length == n - 10 <= edges[i][0], edges[i][1] < n0 <= k <= 104
思路:
floor(coins[i] / 2) 等价于 coins[i] >> 1。
右移运算是可以叠加的,即 (x >> 1) >> 1 等于 x >> 2。
我们可以在递归的过程中,额外记录从根节点递归到当前节点的过程中,一共执行了多少次右移,也就是子树中的每个节点值需要右移的次数。
故定义 dfs(i,j) 表示递归到以 i 为根的子树,在上面已经执行了 j 次右移的前提下,我们在这棵子树中最多可以得到多少积分。
用「选或不选」来思考,即是否执行右移:
不右移:答案为 (coins[i] >> j)−k 加上 i 的每个子树 ch 的 dfs(ch,j)。
右移:答案为 coins[i] >> (j+1) 加上 i 的每个子树 ch 的 dfs(ch,j+1)。
两种情况取最大值,得
dfs(i,j) = max
(coins[i] >> j)−k+∑ch dfs(ch,j)
(coins[i] >> (j+1))+∑ch dfs(ch,j+1)
递归入口:dfs(0,0)。其中 i=0 表示根节点。一开始没有执行右移,所以 j=0。
细节
一个数最多右移多少次,就变成 0 了?
设 w 是 coins[i] 的二进制长度,那么 coins[i] 右移 w 次后就是 0 了。
在本题的数据范围下,w≤14。
所以如果在递归过程中发现 j+1=14,就不执行右移,因为此时 dfs(ch,j+1) 子树中的每个节点值都要右移 14 次,算出的结果一定是 0。既然都知道递归的结果了,那就不需要递归了。
此外,为避免错把父亲当作儿子,可以额外传入 fa 表示父节点,遍历 i 的邻居时,跳过邻居节点是 fa 的情况。
代码:
class Solution {
public:
int maximumPoints(vector<vector<int>>& edges, vector<int>& coins, int k) {
int n = coins.size();
vector<vector<int>> g(n);
for (auto& e: edges) {
int x = e[0], y = e[1];
g[x].push_back(y);
g[y].push_back(x);
}
array<int, 14> init_val;
ranges::fill(init_val, -1); // -1 表示没有计算过
vector memo(n, init_val);
auto dfs = [&](this auto&& dfs, int i, int j, int fa) {
int& res = memo[i][j]; // 注意这里是引用
if (res != -1) { // 之前计算过
return res;
}
int res1 = (coins[i] >> j) - k;
int res2 = coins[i] >> (j + 1);
for (int ch : g[i]) {
if (ch == fa) continue;
res1 += dfs(ch, j, i); // 不右移
if (j < 13) { // j+1 >= 14 相当于 res2 += 0,无需递归
res2 += dfs(ch, j + 1, i); // 右移
}
}
return res = max(res1, res2); // 记忆化
};
return dfs(0, 0, -1);
}
};