题目:
一张桌子上总共有 n 个硬币 栈 。每个栈有 正整数 个带面值的硬币。
每一次操作中,你可以从任意一个栈的 顶部 取出 1 个硬币,从栈中移除它,并放入你的钱包里。
给你一个列表 piles ,其中 piles[i] 是一个整数数组,分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ,请你返回在 恰好 进行 k 次操作的前提下,你钱包里硬币面值之和 最大为多少 。
示例 1:
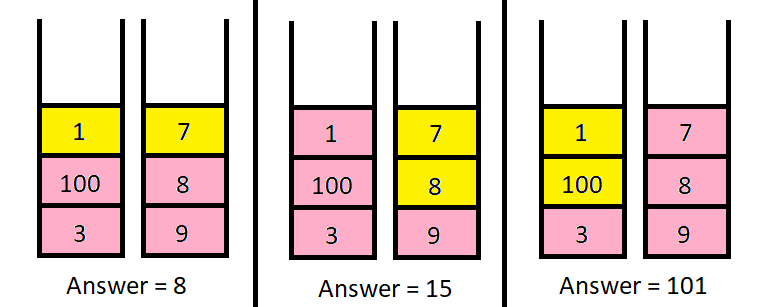
输入:piles = [[1,100,3],[7,8,9]], k = 2
输出:101
解释:
上图展示了几种选择 k 个硬币的不同方法。
我们可以得到的最大面值为 101 。
示例 2:
输入:piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
输出:706
解释:
如果我们所有硬币都从最后一个栈中取,可以得到最大面值和。
提示:
n == piles.length1 <= n <= 10001 <= piles[i][j] <= 1051 <= k <= sum(piles[i].length) <= 2000
思路:
对于一个栈(数组),我们只能移除其前缀。注意题目说数组 piles[i] 从左到右表示栈顶到栈底。
对每个栈求前缀和 s,其中 s[w] 表示一个体积为 w+1,价值为 s[w] 的物品。
问题转化成:
从 n 个物品组中选物品,每组至多选一个物品(可以不选),要求体积总和至多为 k,求物品价值总和的最大值。
⚠注意:对于本题来说,由于元素值都是非负数,且一定可以选 k 个硬币,所以「至多」和「恰好」计算出来的结果是一样的。为方便写代码这里用至多。
记忆化搜索
类似 0-1 背包,定义 dfs(i,j) 表示从 piles[0] 到 piles[i] 中,选体积之和至多为 j 的物品时,物品价值之和的最大值。
枚举第 i 组的所有物品(枚举前缀和),设当前物品体积为 w,价值为 v,那么问题变成从前 i−1 个物品组中,选体积之和至多为 j−w 的物品时,物品价值之和的最大值,即 dfs(i−1,j−w),加上 v 得到 dfs(i,j)。
所有情况取最大值,得 dfs(i,j)= (v,w)max dfs(i−1, j−w) + v
如果该组不选物品,则上式中的 v=w=0。
递归边界:dfs(−1,j)=0。
递归入口:dfs(n−1,k),这是原问题,也是答案。
代码:
class Solution {
public:
int maxValueOfCoins(vector<vector<int>>& piles, int k) {
int n = size(piles);
vector memo(n, vector<int>(k + 1));
auto dfs = [&](this auto&& dfs, int i, int j) -> int {
if (i < 0) {
return 0;
}
int& res = memo[i][j]; // 注意这里是引用
if (res) { // 之前计算过
return res;
}
// 不选这一组中的任何物品
res = dfs(i - 1, j);
// 枚举选哪个
int v = 0;
for (int w = 0; w < min(j, (int) piles[i].size()); w++) {
v += piles[i][w];
// w 从 0 开始,物品体积为 w+1
res = max(res, dfs(i - 1, j - w - 1) + v);
}
return res;
};
return dfs(n - 1, k);
}
};